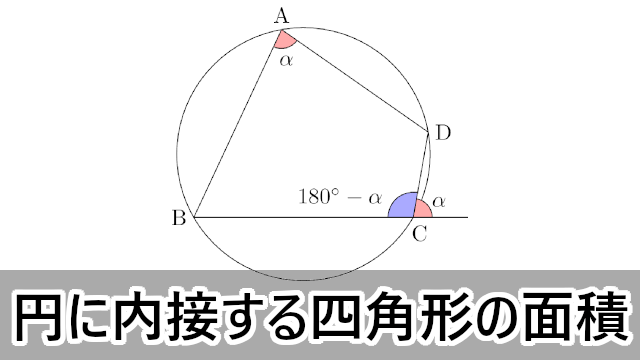
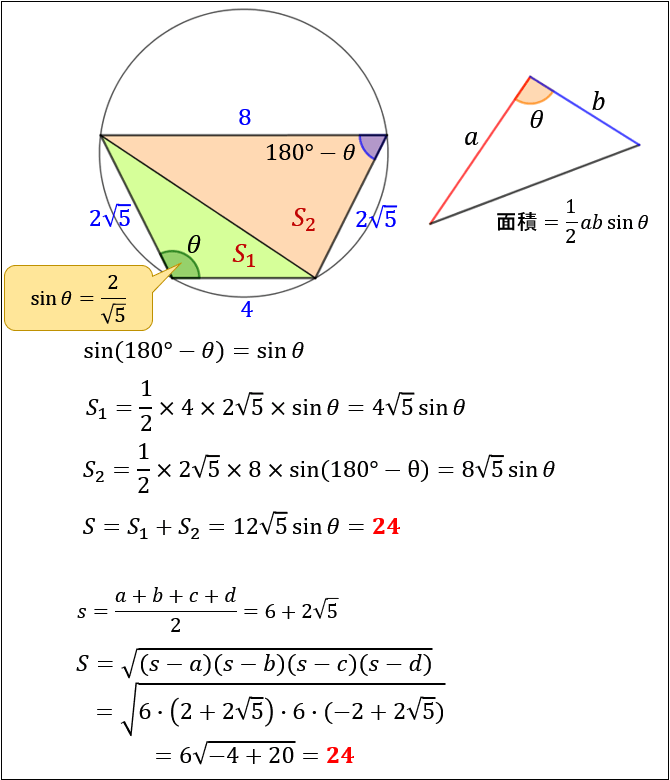
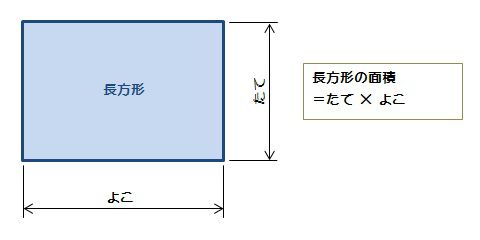
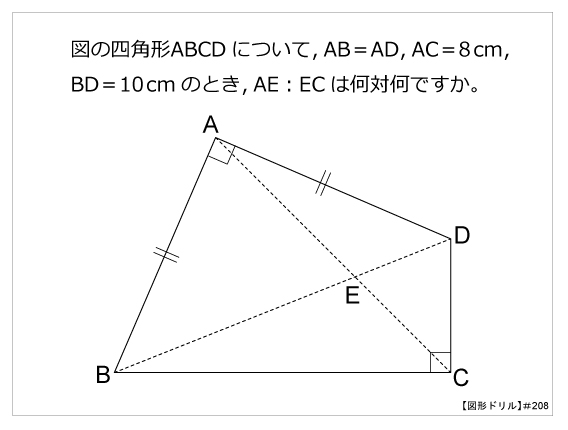
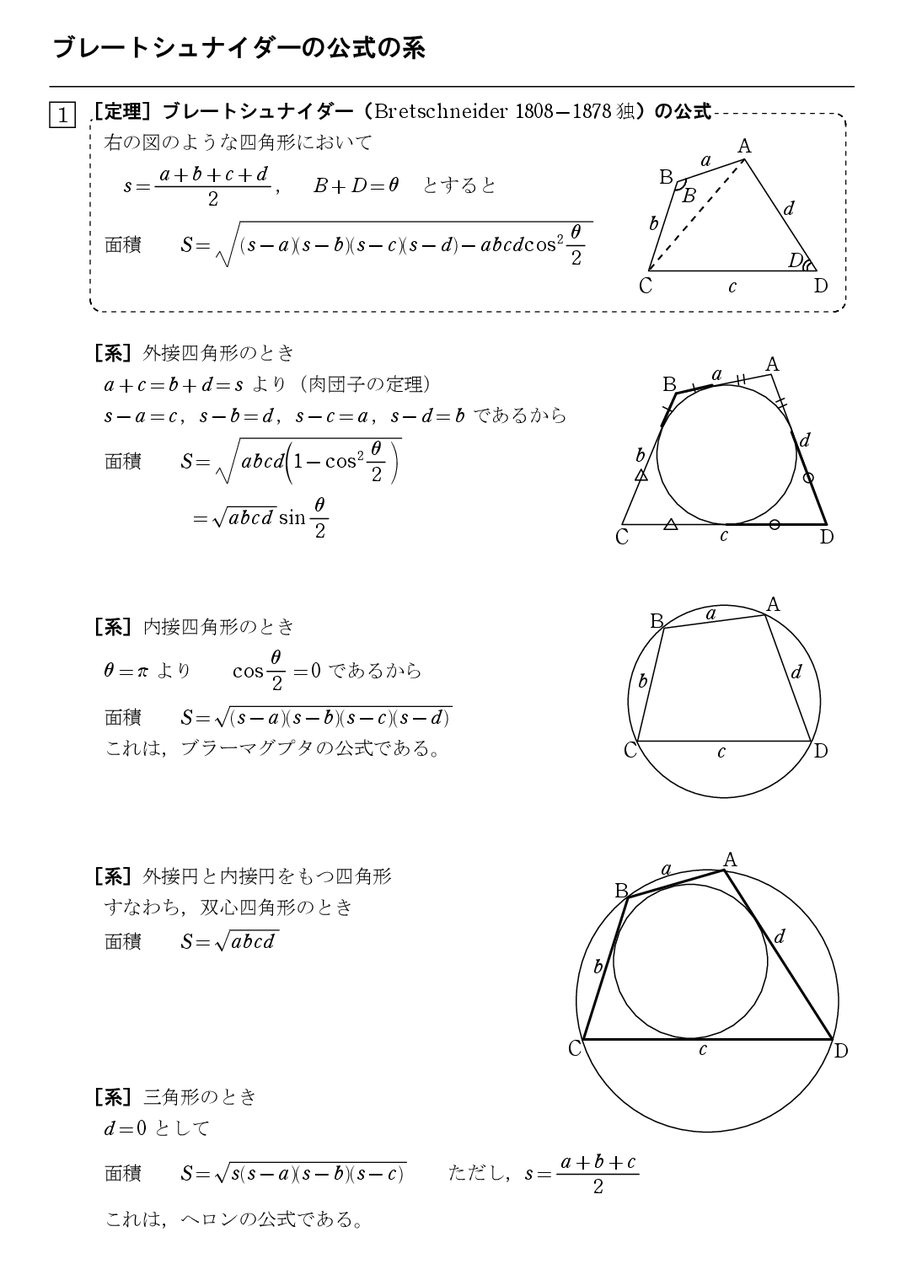
概要 ブラーマグプタの公式は、7世紀にインドの数学者 ブラーマグプタがヘロンの公式の一般化として得た定理である。 ヘロンの公式は三角形の3辺の長さから三角形の面積を求める公式であるが、ブラーマグプタの公式は四角形の 4辺の長さから四角形の面積を求める公式である。
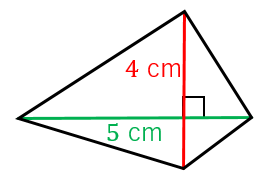
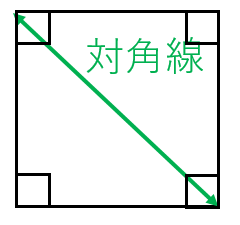
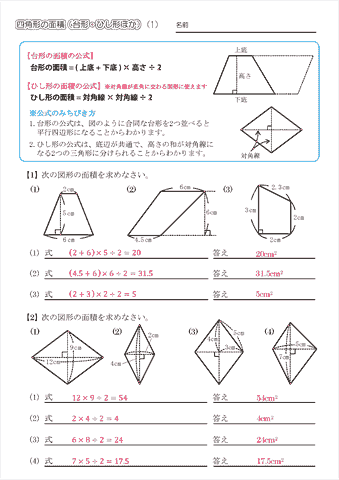
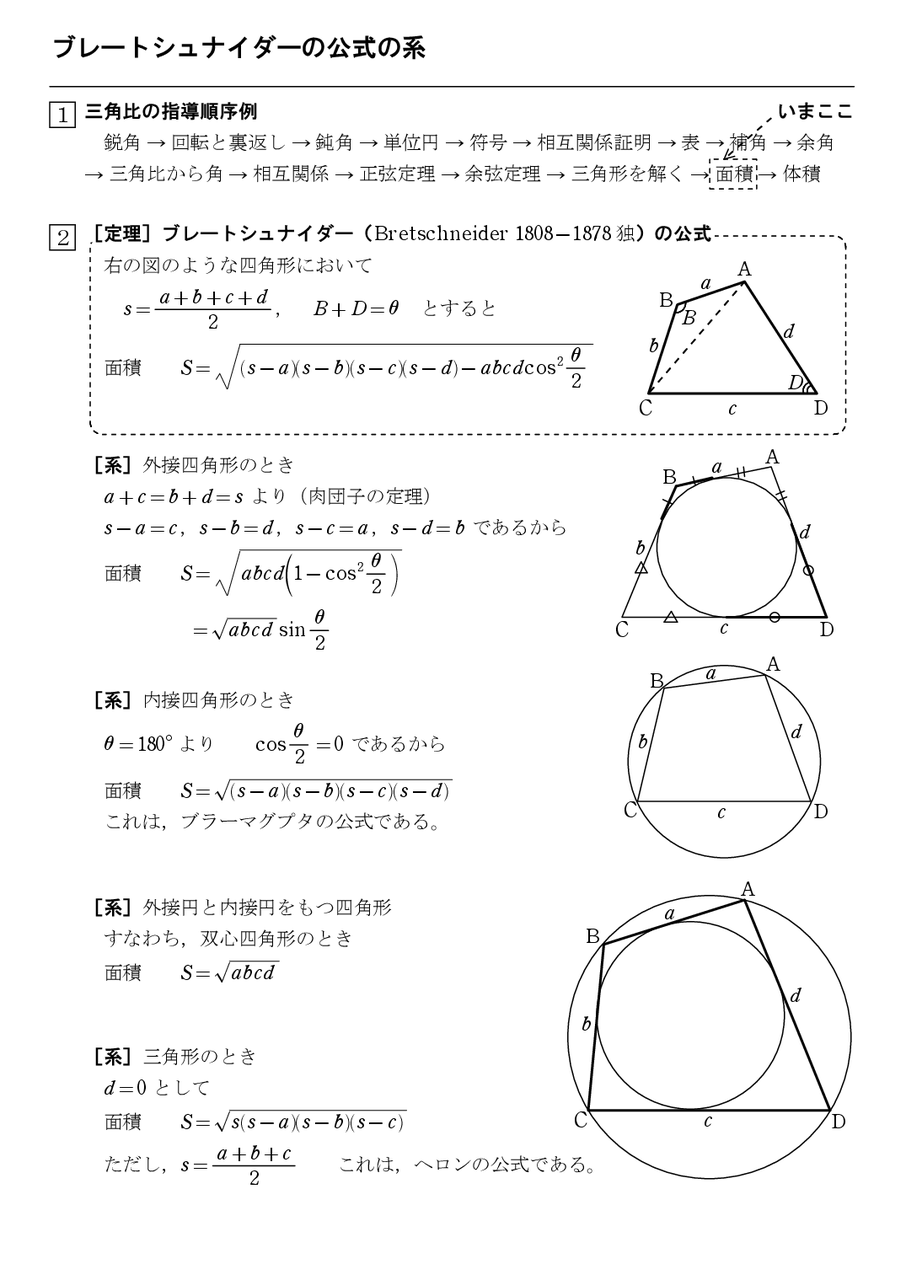
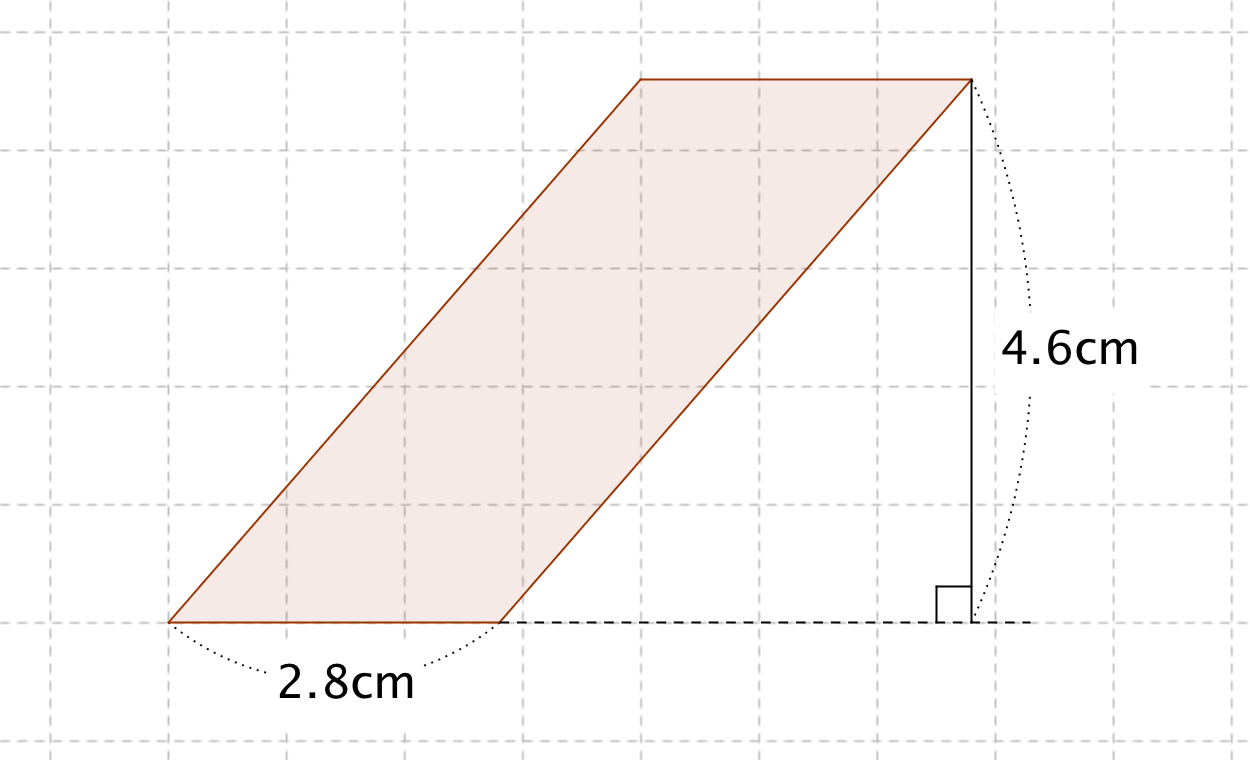
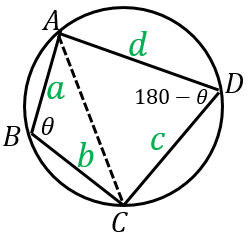
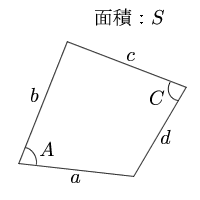
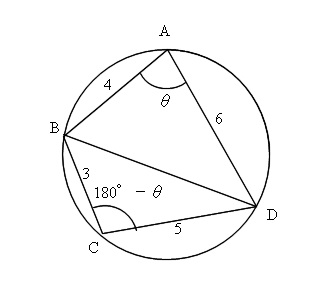
四角形の面積の公式 求め方- 四角形の面積にまつわる公式 ブラーマグプタの公式とその証明 円に内接する四角形の面積をヘロンと同じノリで求める有名な公式です。 ブレートシュナイダーの公式 ブラーマグプタの公式の一般化です。これはあくまで観賞用ですかね。 四角形を 2 つの三角形に分けて 、三角形の面積の公式「 \displaystyle S = \frac {1} {2} bc \sin \mathrm {A} 」で面積を表します。 ヘロンの公式の証明と同様、三角比の相互関係と余弦定理を用いて三角比を辺の長さで表現すれば証明できます。 証明 (見切れる場合
四角形の面積の公式 求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  | |
 |  | |
「四角形の面積の公式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  |  |
「四角形の面積の公式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「四角形の面積の公式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
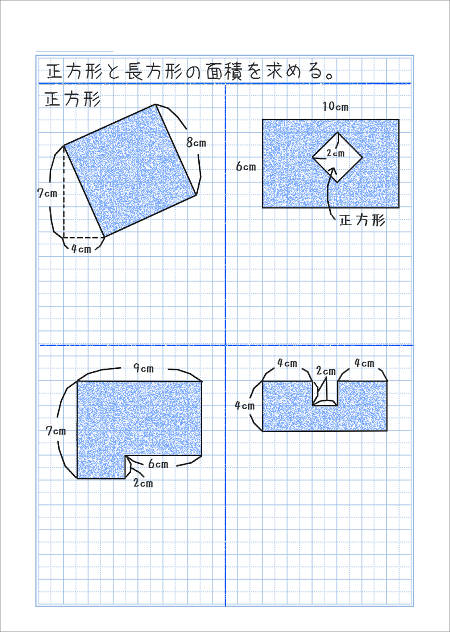 |  | |
「四角形の面積の公式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
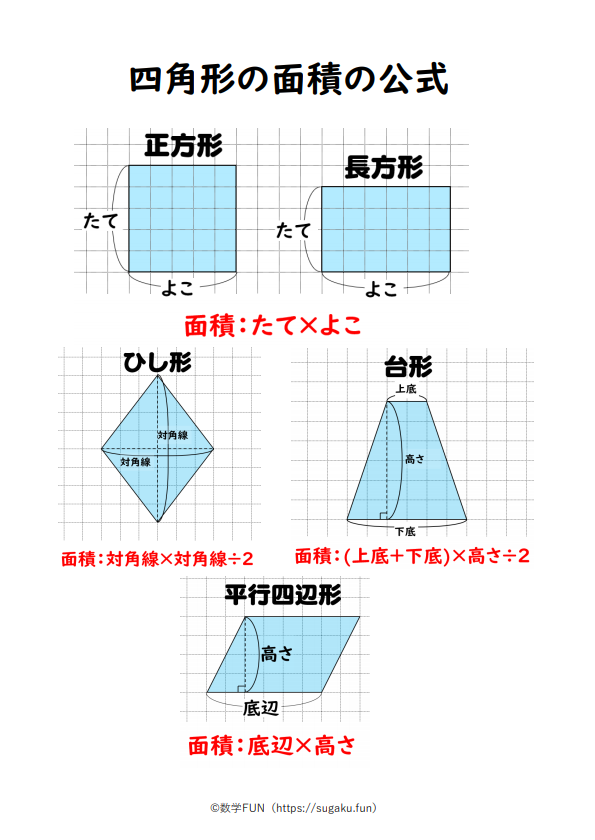
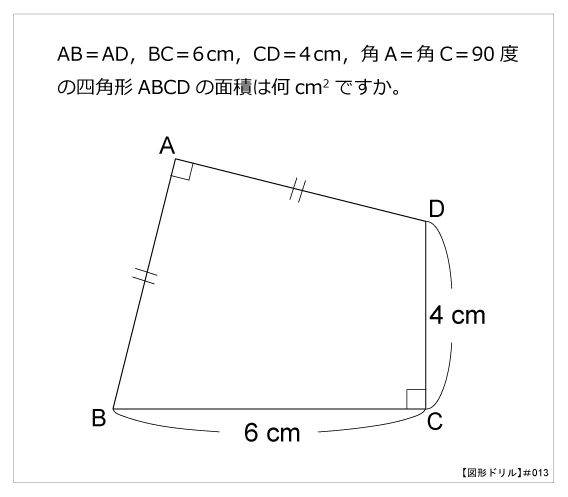 |  | |
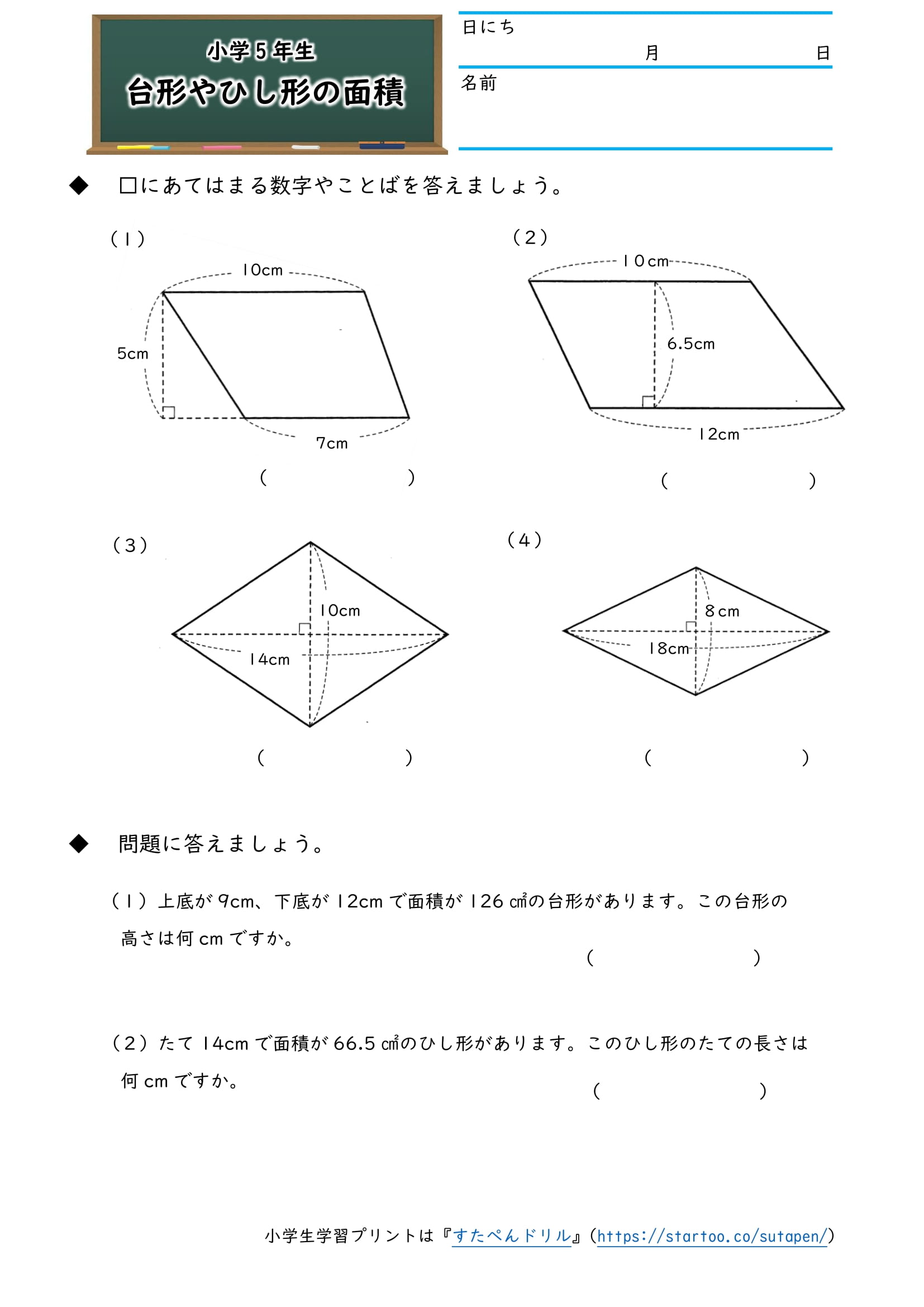 | 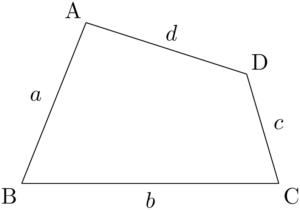 | 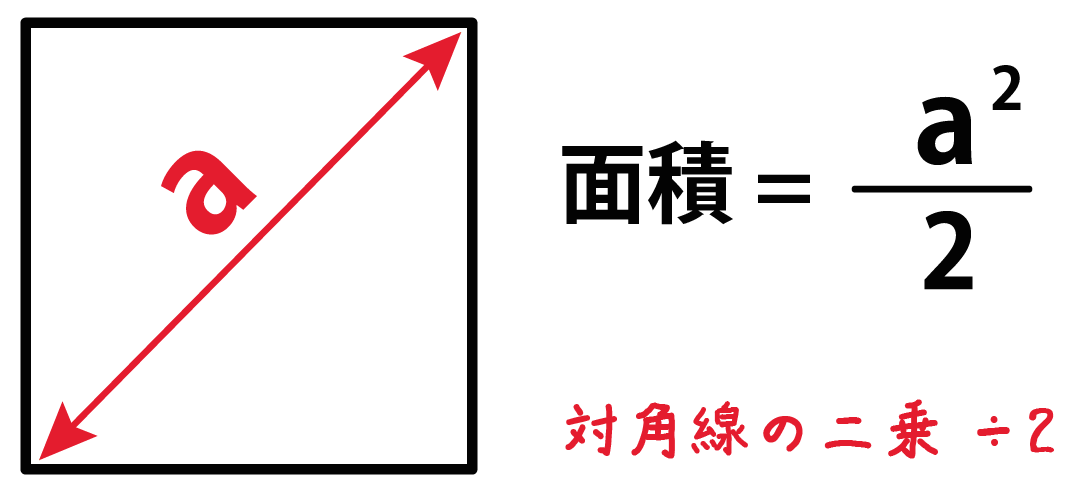 |
 |  |  |
 |  |  |
「四角形の面積の公式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「四角形の面積の公式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「四角形の面積の公式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
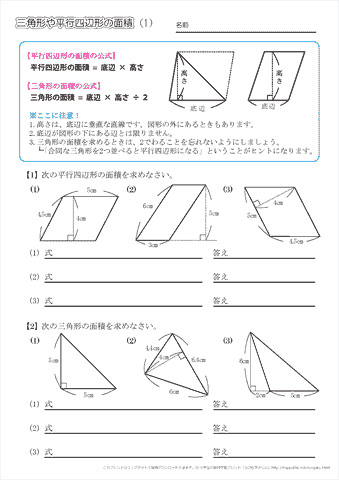 | 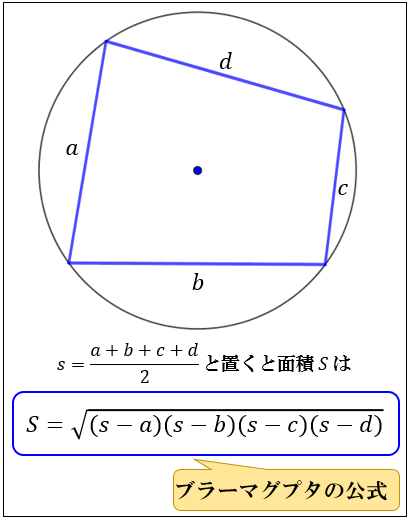 | |
 |  |  |
「四角形の面積の公式 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
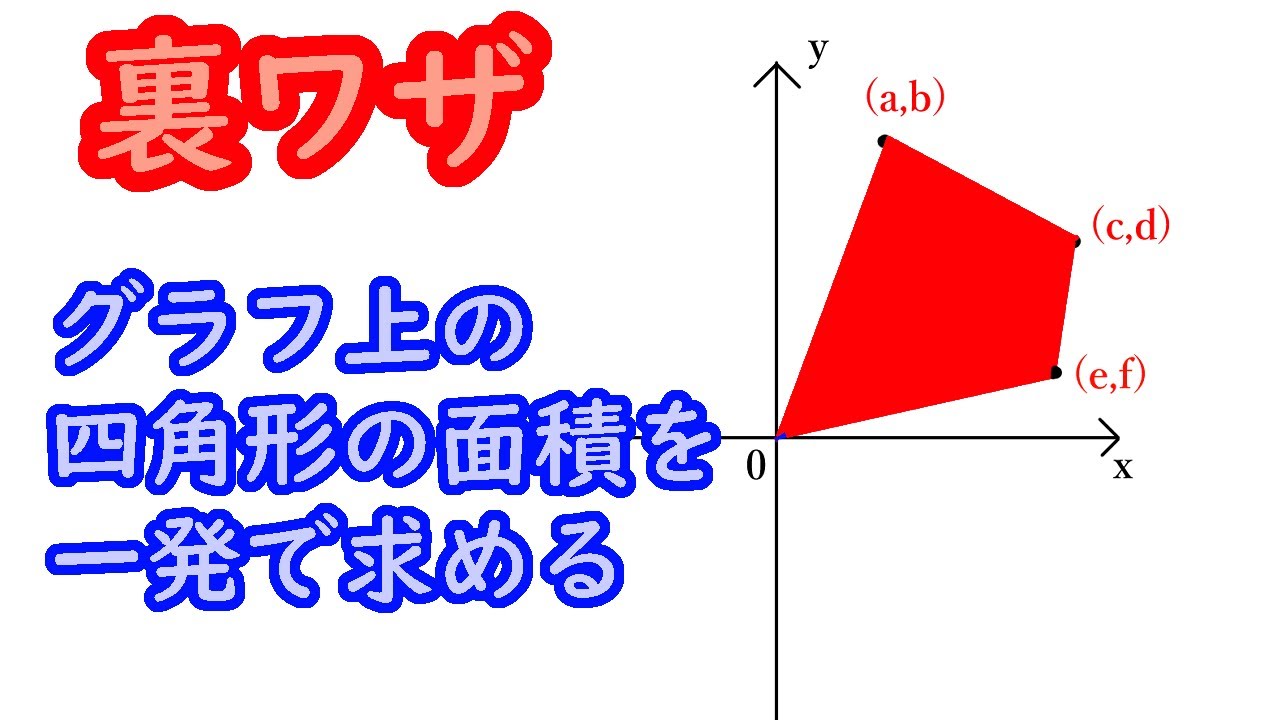
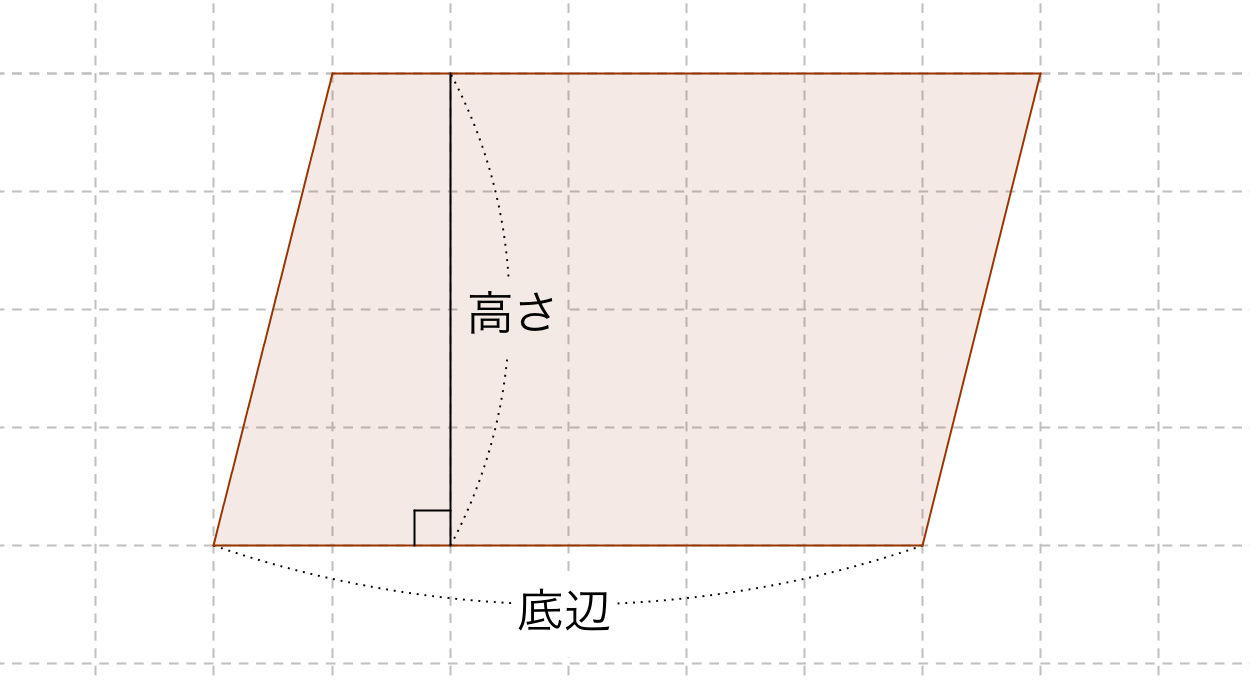 |  | |
 |  | |
 |  |
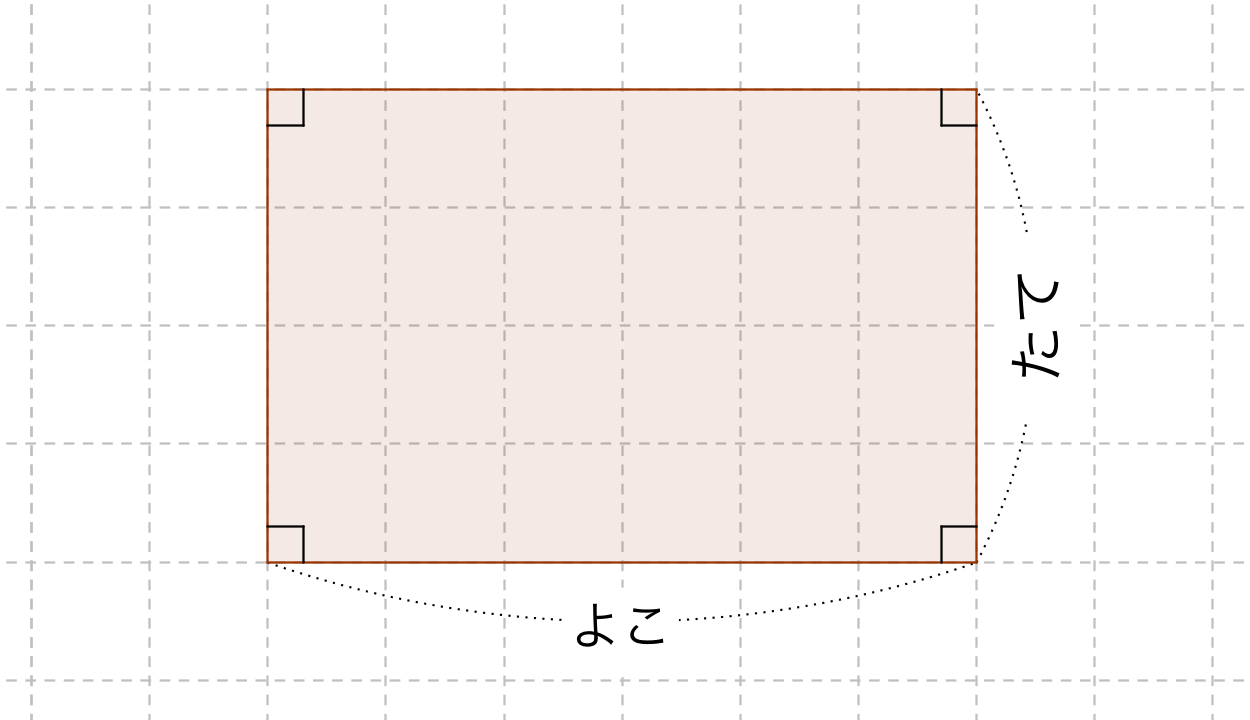
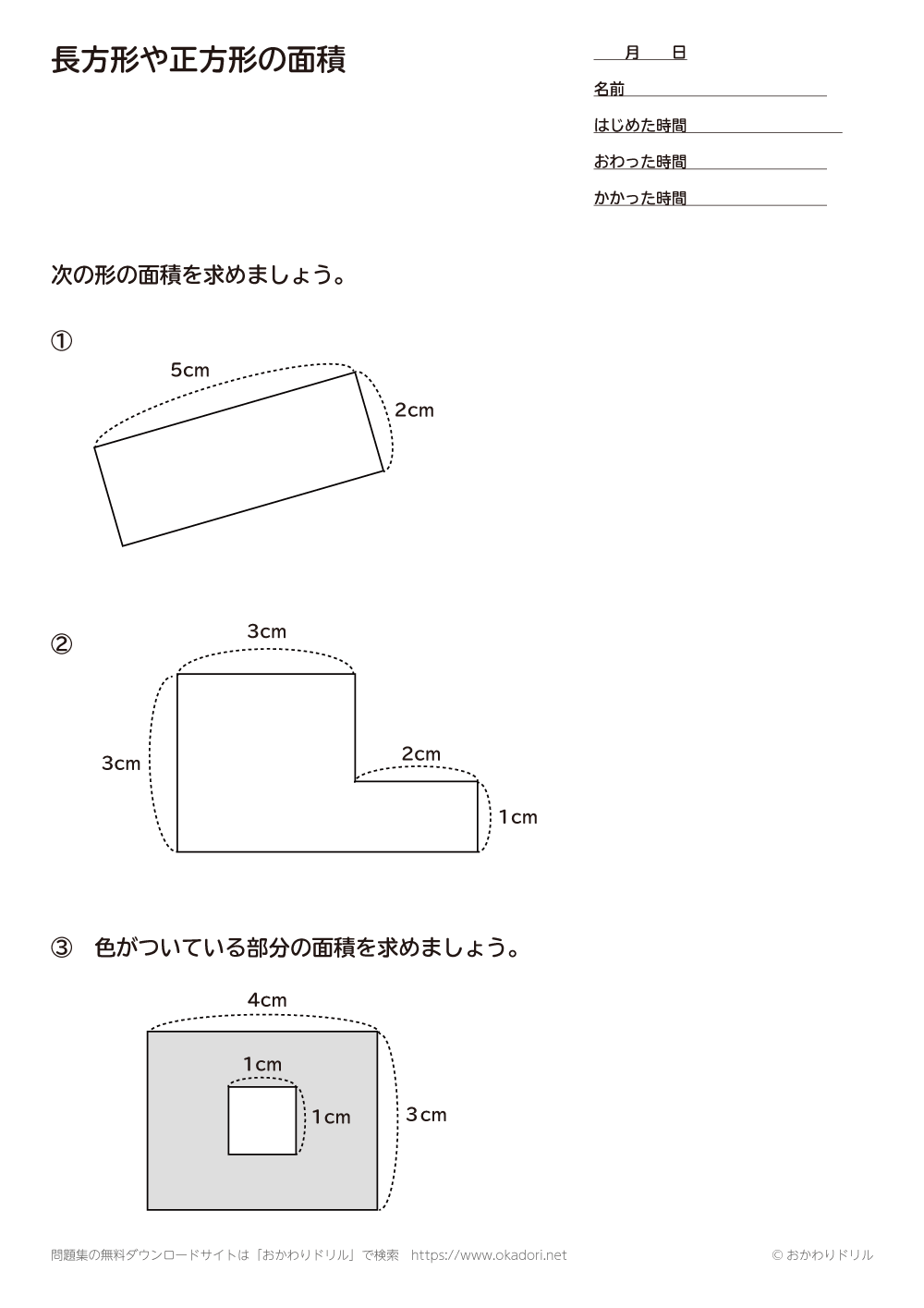
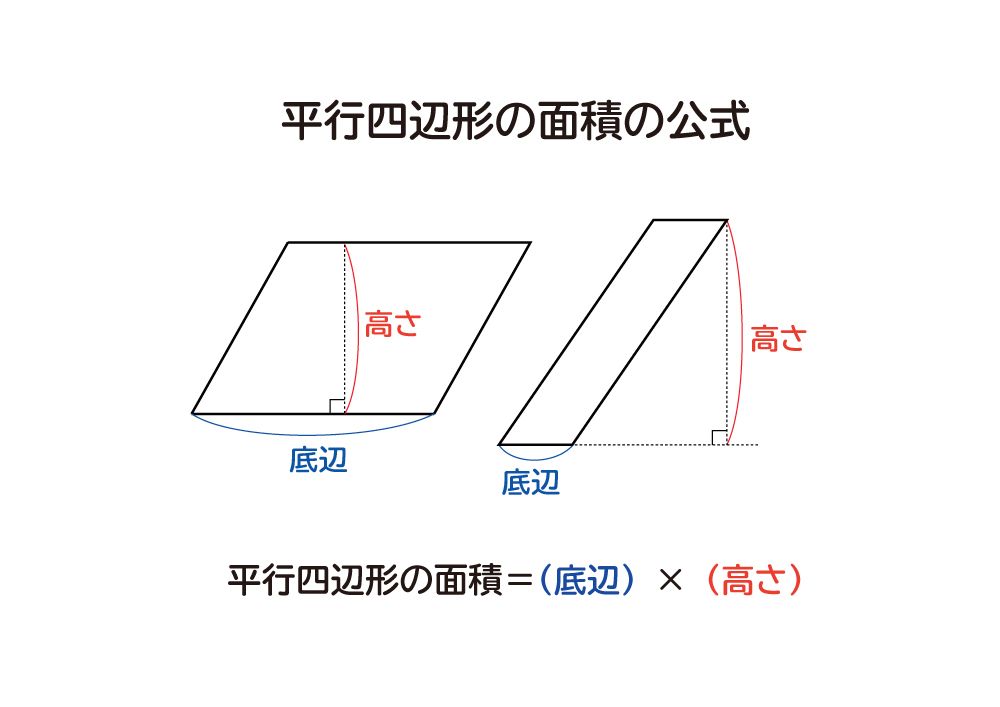
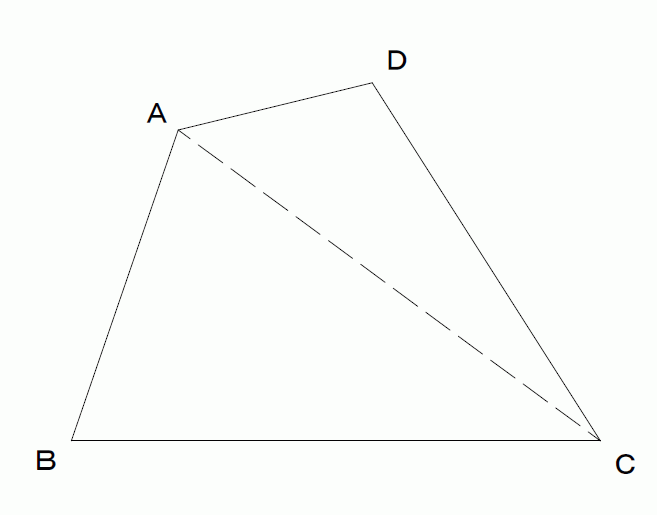
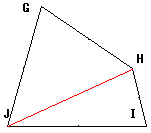
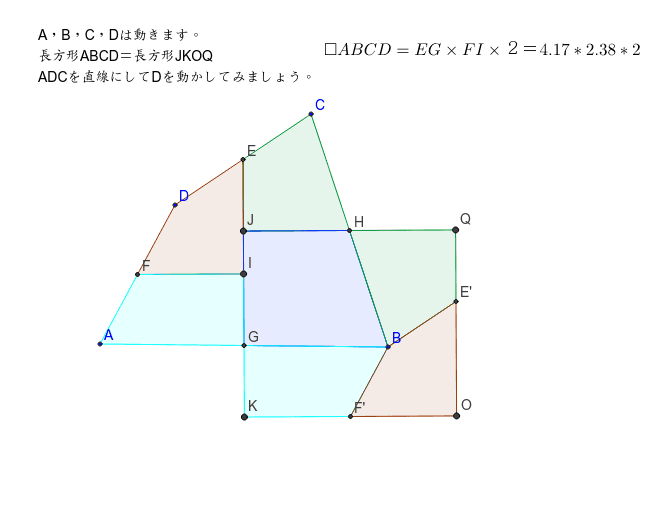
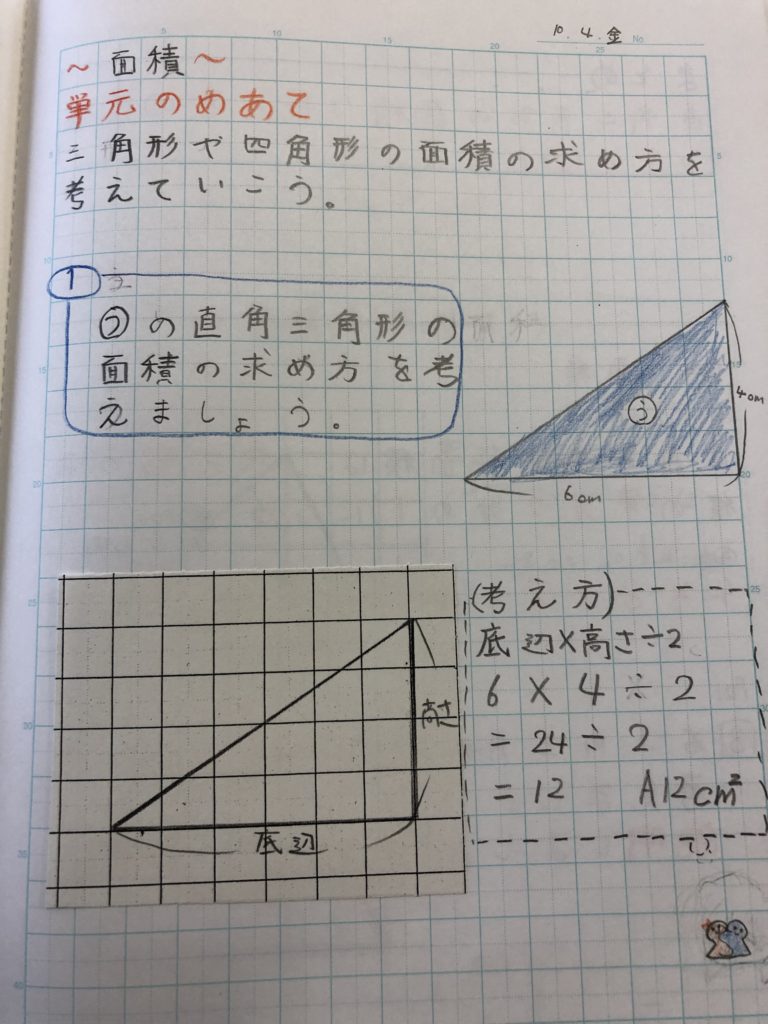
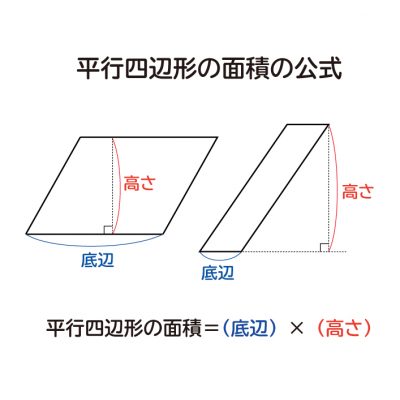
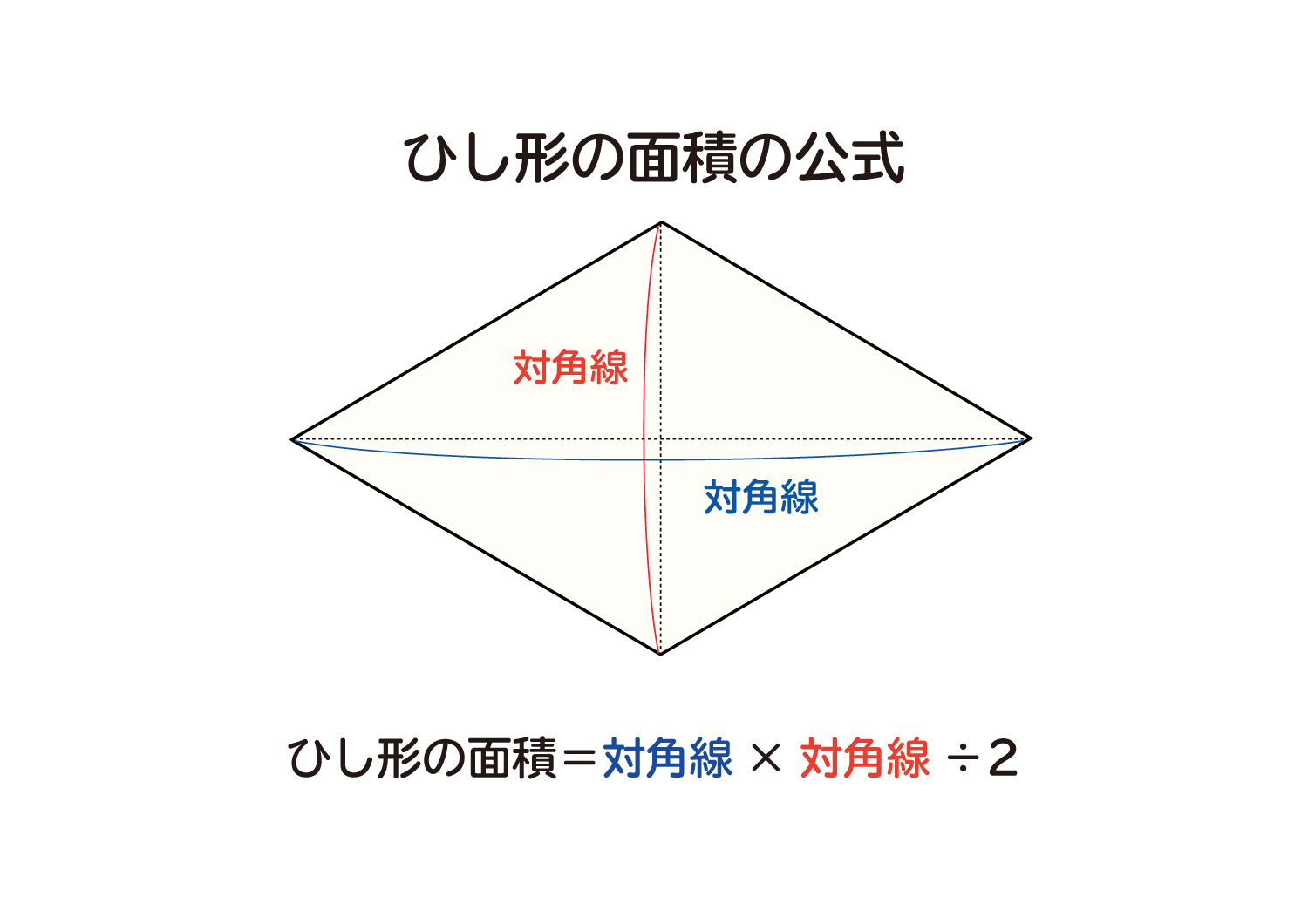
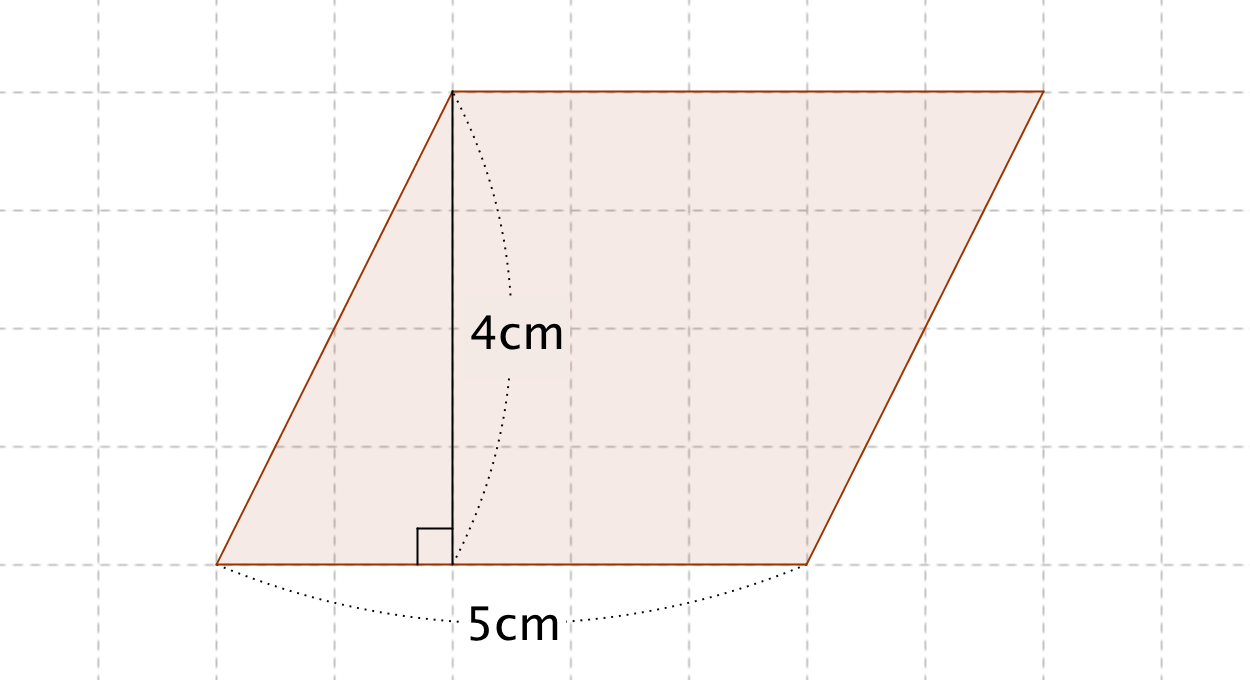
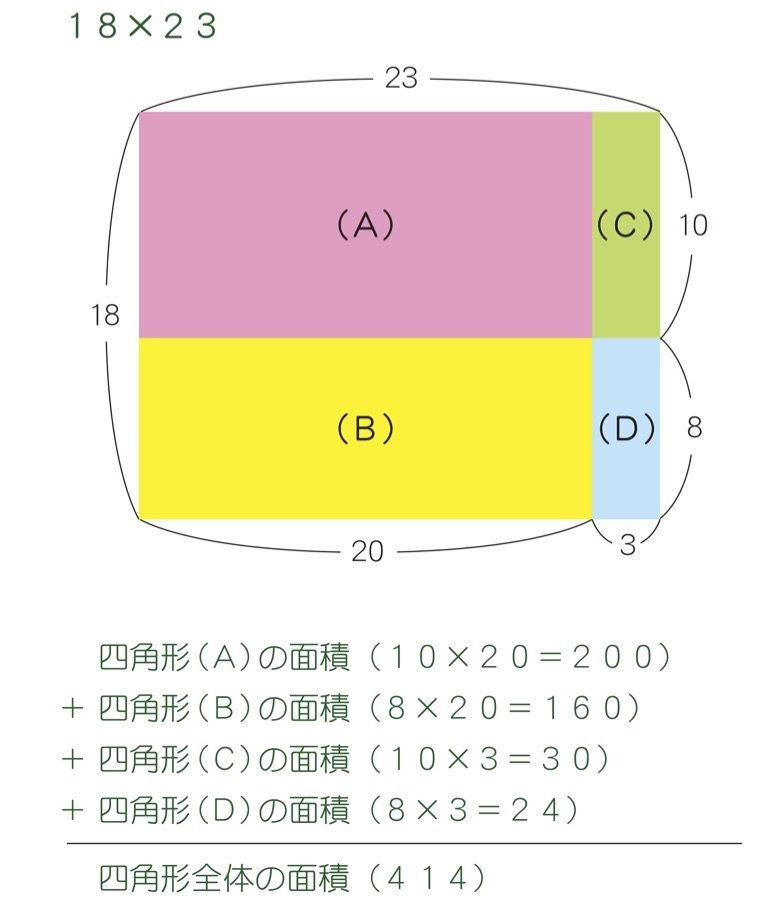
四角形の面積の公式 The area formula of the quadrilateral;さて、この四角形の面積を求めるには普通どう考える? S:二つの三角形に分けます。 三角形なら公式が使えるから。 S:この四角形をJHで分けて、JHからの高さをそれぞれhとiとすると、 面積=JH×(h+i)÷2 で求まるよ。 T:でもね、この公式からは
Incoming Term: 四角形の面積の公式, 四角形の面積の公式 高校, 四角形の面積の公式 小学生, 四角形の面積の公式 対角線, 四角形の面積の公式 証明, 四角形の面積の公式 正方形, 四角形の面積の公式 求め方, 円 四角形の面積の公式,



