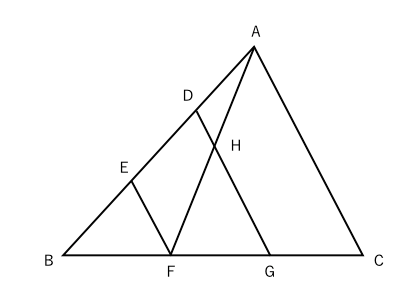
補助線(ほじょせん)をひいてみたら、次のように比がわかりました。 最後に整理して図にかくとこうなりました。 だから、三角形bhg の面積と 三角形bdf の面積の比は? ( 4 ×三角形DEHと三角形GHFの面積はそれぞれ 9cm 2 。 また、三角形DBE、三角形GFCもそれぞれ15cm 2 になる。 よって、台形DBCGの面積は6+135+9+9+15+15 =675cm 2 。 三角形ABCと三角形ADGの面積の比は1:4。 台形DBCGは3にあたり、三角形ADGの面積は225cm 2 。こちら の記事で説明したように、 三角形の面積比は「(底辺の比)×(高さの比)」 で求めます。

大至急です 相似 面積比の問題です Clear
面積の比 三角形
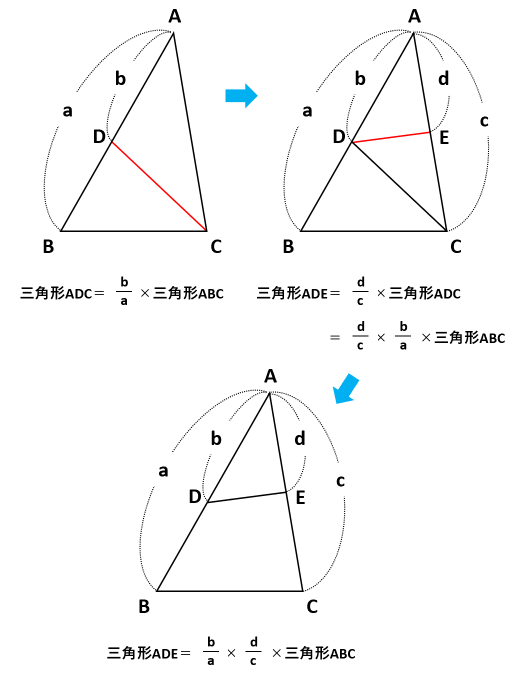
面積の比 三角形-2 n ×1角共有の三角形の面積比 解説 次の図の abcと adeのように,1つの角(∠a)が共有されている2つの三角形の面積比について考えます。




平面図形をマスター 三角形の面積比 応用編その2
面積比の公式3選とは三角形 さて、今までの話を踏まえ、ここからは「 相似じゃない図形の面積比 」について考えていきます。 具体的には 高さが等しい三角形;今回の学習 第27回 第3章 三角比三角形の頂点から対辺の中点にひいた線分は,三角形の面積を二等分する 例1 3点 A(3, 4), B(1, 2), C(5, 0) を頂点とする ABC がある.
よって、「正確な面積の数値」が無くても「高さの比」や「底辺の比」だけで 2つの三角形の「面積比」がわかるということにつながりますね! 元の面積を「s」とすれば、 ・多角形の場合 多角形は三角形分割できます。図形を k k k 倍に拡大すると,各三角形の面積は k 2 k^2 k 2 倍になるので全体の面積も k 2 k^2 k 2 倍になります。 一般の図形の場合(大雑把な説明) 一般の図形は(無限に小さい)長方形に分割できます。2 = N じゃから、 (三角形ABDの面積):(三角形ACDの面積)= m ×
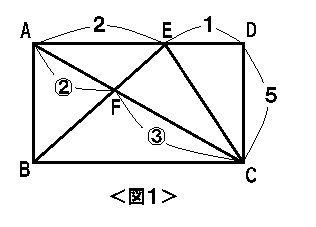
2 ) : ( 5 ×三角形fdgとadcは相似。相似比2:3なので 面積比④ :⑨ 台形abcdの面積比は⑱ 5)abef=abcgfcge①、abcgf=abcd⑱ーfdg④=⑭、 abef=⑮ (⑭+①) 台形abefと三角形fgdの面積比を最も簡単な整数の比で表してください。 答え)15:4 まとめ 三角形が相似の場合対角線の比=面積比 今までの単純な底辺比にプラス 四角形を対角線で分割した三角形の面積比から、高さにあたる対角線の分割比を求める。 ((図)) これを使います。 交差切りの図



面積が何倍かを求める問題 応用編 苦手な数学を簡単に




平面図形をマスター 三角形の面積比 応用編その3
3 ) = 8 : 15 となり、海城中三角形の面積比 21年 21年 6年生 入試解説 東京 男子校 面積比 ★★★★☆☆(中学入試難関校レベル) 印象に残った入試問題の良問を「今年の1問」と題して取り上げています。 志望校への腕試しや,重要項目の確認に是非ご活用下さい。最後の三角形の問題の2つに分ける線が3つでその下の台形と1番上の三角形の面積比を求める場合は、、、? Ken より 19年1月8日 1005 AM
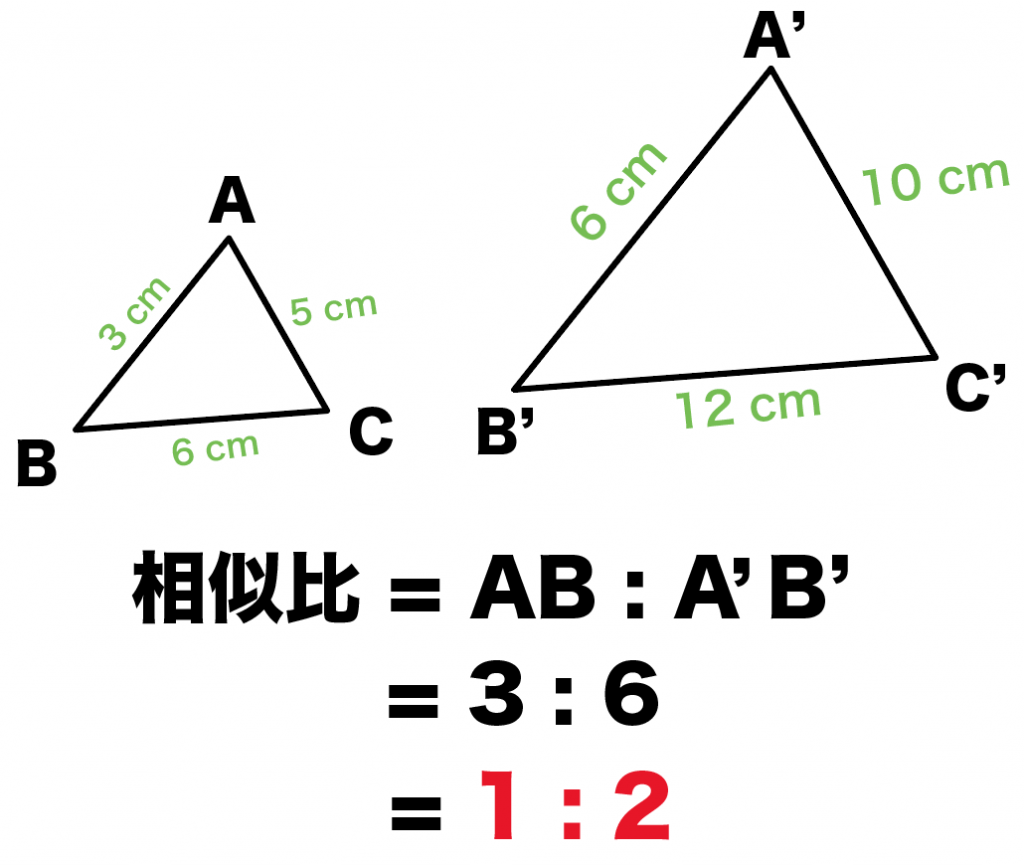



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく
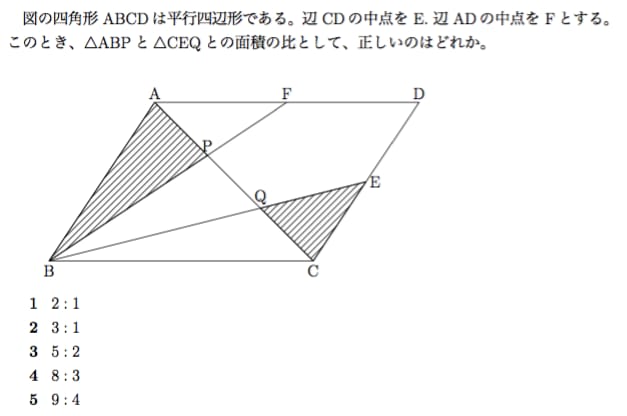



平行四辺形 中点 2つの三角形の面積比 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください
高さが等しい三角形→底辺比=面積比 なので、三角形に分けられた図形の面積比を考える場合、高さが同じ三角形を 探し、それらの組み合わせに注目するというテクニックがあります。 図の出典:『塾技100』p136\( \frac{三角形ABX}{三角形ACX} = \frac{BD}{CD} \) ・・・(式1) となるわけじゃ(この式を、式1、と名前をつけておくかのぉ) 次に、別の面積比を考えてみるかのぉ ピンクと緑の面積比は、AFとBFの線分比で表現できるわけじゃあとは面積比を考えればおしまいですね。辺の比が分かっているので、面積比も求めることができます。 三角形 ABC の面積を S とすると、 $\mathrm{ BD }\mathrm{ DC }=54$ なので、三角形 ABD の面積は $\dfrac{5}{9}S$ 、三角形 ACD の面積は $\dfrac{4}{9}S$ となります。



三角形 四角形の面積比 中学から数学だいすき
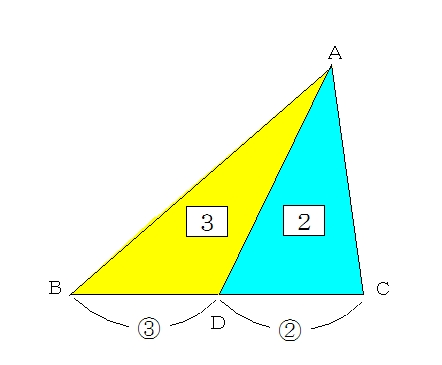



辺の比と面積比
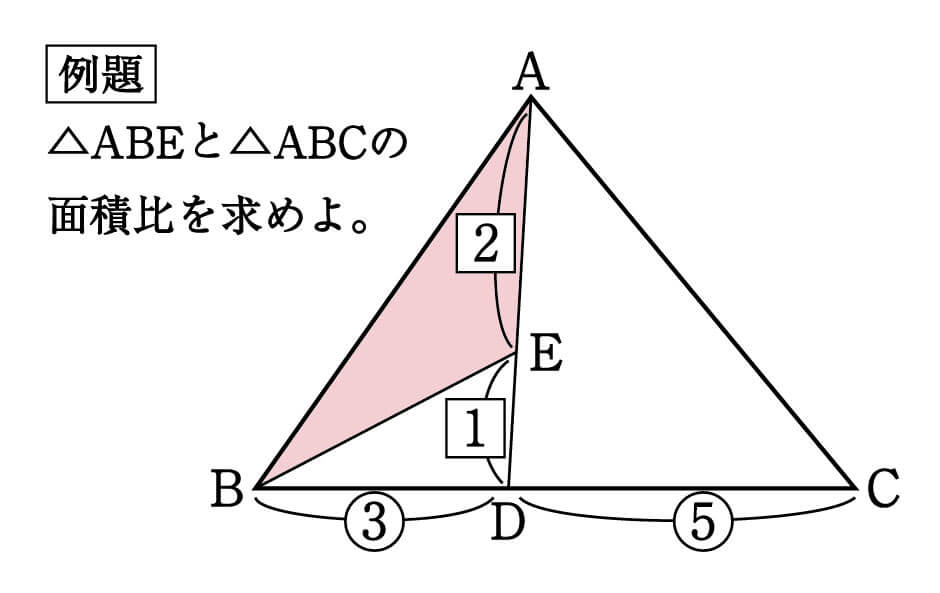
底辺比2:3が2つの三角形の面積比になる。三角形adeが9なので三角形abeは6と分かる。 三角形の面積比は求められました。最後に右側の四角形部分です。 5合同な三角形から四角形の面積比 平行四辺形の左上と右下で、2つの三角形にわけてみます。算数 三角形と四角形の面積比 小学生 算数のノート Clear 表紙 1 2 公開日時 21年08月13日 09時18分 更新日時 21年08月27日 04時46分 小学生 算数練習問題に挑戦! まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! こちらの関連記事はいかがでしょうか?




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題



辺の比と面積比
一行目に「⊿ adp ∽⊿ ebp だから」とあるけれど、まず解答でこの三角形の相似に着目したことがすんなりと理解できるだろうか? 説明できるか? 求めたい⊿はオレンジで囲った部分と緑で囲った部分だよ。しかも面積比を求めろと言っているのに、ここから⊿ adp ∽⊿ ebp の相似に注目しよう台形abcdがあり、上底adと下底bcの比は2:3です。 台形の面積が50cm 2 であるとき、 aobの面積はいくつでしょうか? という問題です。 問題文には‟面積比"という言葉が使われていませんが、2つの異なる図形の面積を比べる問題なので、これも面積比のパターンの1つです。2つの三角形が背中合わせに、横に並んでいるパターンです。 この場合、どちらの三角形も高さは同じ。 ということは、2つの三角形の面積比は、底辺の比率と同じであるといえますよね。 高さが共通の隣り合う三角形の面積比は底辺比に等しい。
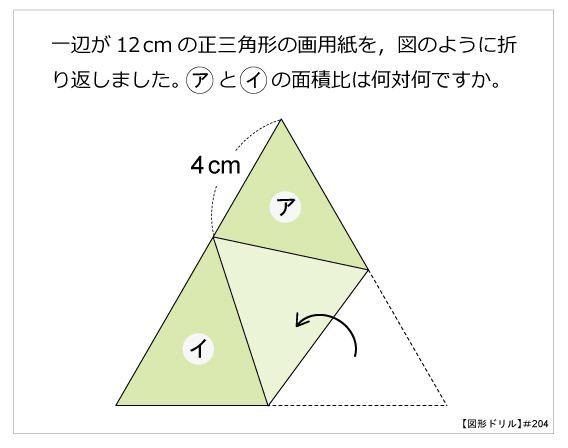



図形ドリル 第4問 正三角形の折り返し 算数星人のweb問題集 中学受験算数の問題に挑戦
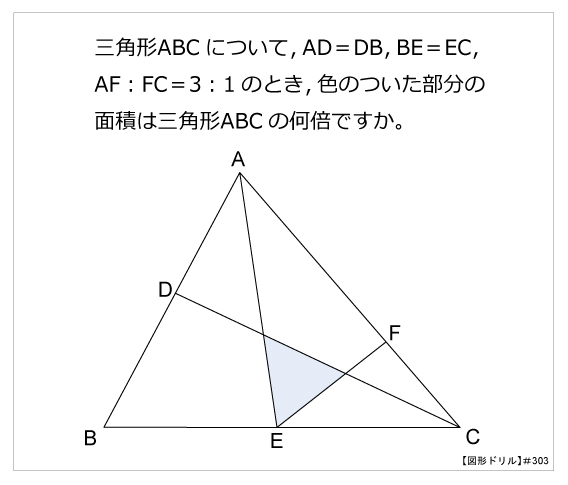



図形ドリル 第303問 三角形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦
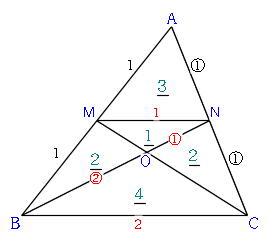
第27回 第3章 三角比 三角形の面積;上野竜生です。三角形の面積比は線分比と密接な関係があります。これについて紹介します。 基本は三角形の面積の公式 三角形の面積の基本の公式は「底辺×高さ÷2」 ということは「底辺」「高さ」が等しい三角形の面積は等しいですし中点連結定理 a b c m n abcの2辺ab, acの中点をそれぞれm, nとすると mn//bc, mn= 1 2 bcとなる。 定理の証明 amnと abcにおいて ∠aは共通(1) mはabの中点なのでamab=12 nはacの中点なのでanac=12 よってamab=anac=12(2)



南山中学女子部過去問題演習
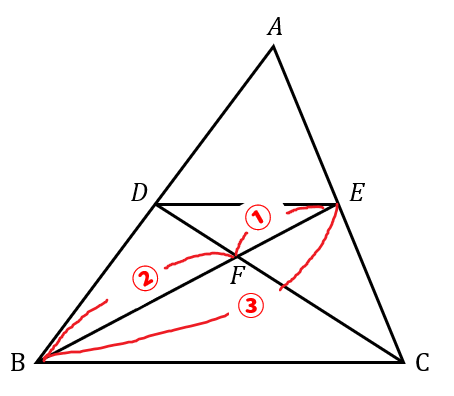



これでバッチリ 相似の面積比を求める問題をイチからやってみよう 数スタ
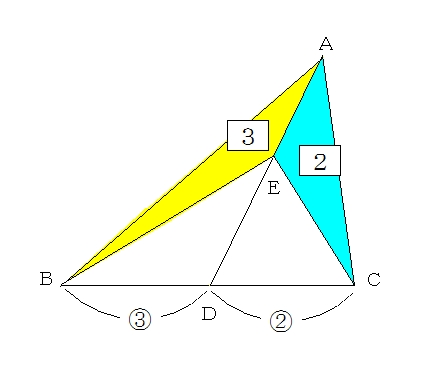
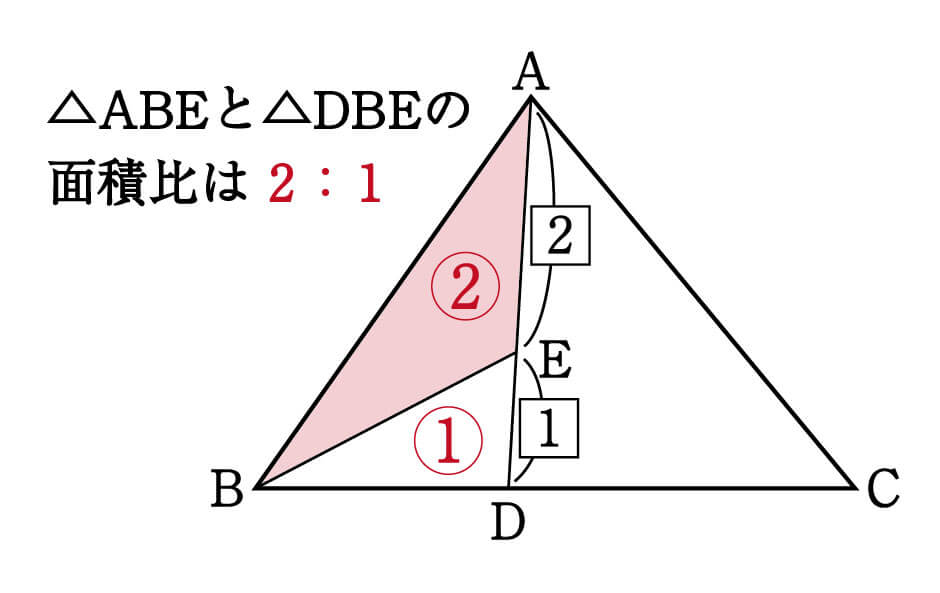
三角形abcと三角形adeで「ひとつの角(角a)が共通(重なっている)」とき、 面積の比はその共通角をはさむ2辺の積、 三角形abcの面積:三角形adeの面積=5×9:2×4=45:8 で求められるというものです。 この解き方を習っている場合は、 ア×3:イ×2=2:1 な底辺比 = 面積比 より、 ef : fc = 2 : 5 であることがわかる。 これより、 三角形efd と 三角形cfb の辺の長さの比は 同じであるから、 df : bf = 2 : 5 である。1 2 1 2 」でしたね。
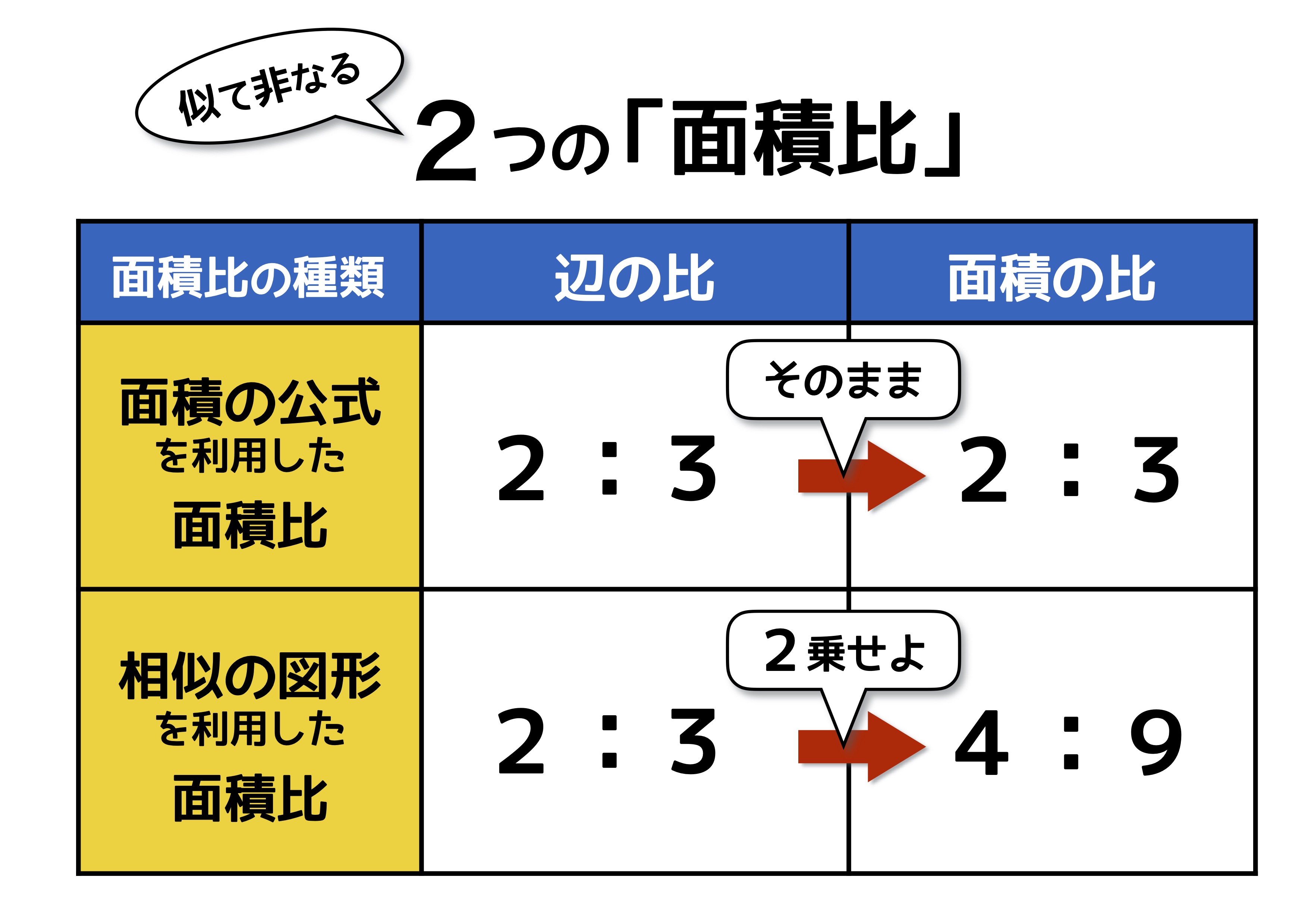



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
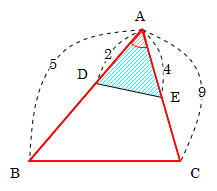



平面図形 辺の比と面積の比 前田昌宏の中学受験が楽しくなる算数塾
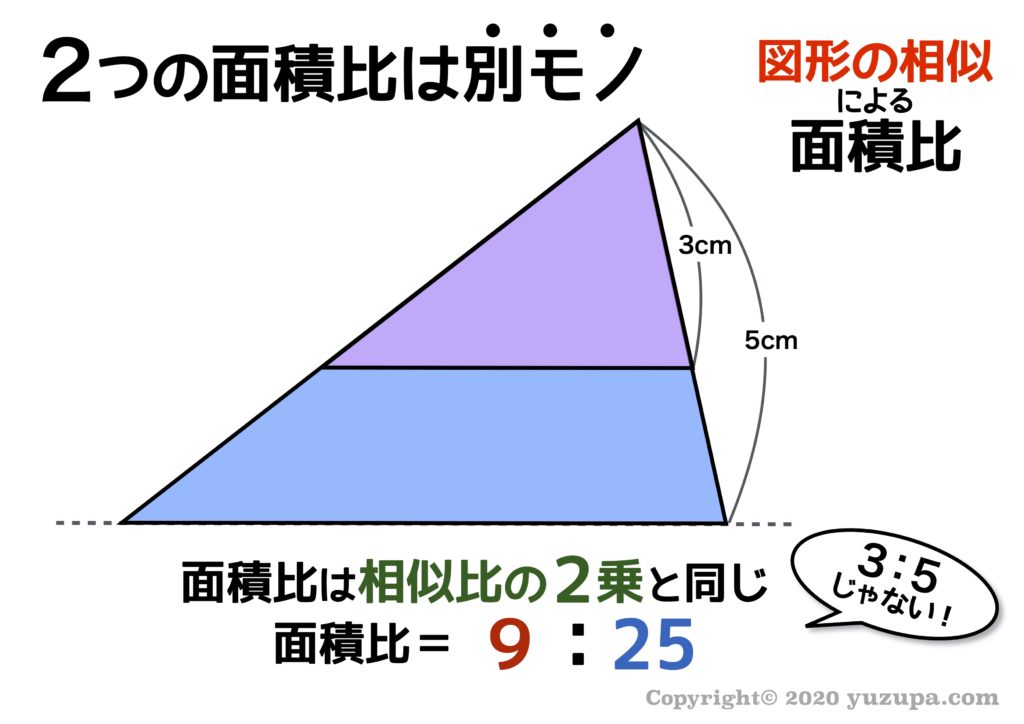
第49回1つの角が等しい三角形の面積比①の授業プリント&授業映像 更新日: 年9月6日 第49回1つの角が等しい三角形の面積比①の授業プリントはこちらから印刷できます。 → 第49回1つの角が等しい三角形の面積比①(問題) 第49回1つの角が等しい三角図の三角形ABCと三角形CEDの面積の比は、 : です。 図で、三角形ABCと三角形CEDの面積の比が 3:5 のとき、CEの長さは何cmですか。2 となるわけじゃ 比があったら、簡単にできるか考えるのが大事じゃな 具体的には、以下のように、できるんじゃな




応用 ベクトルの等式と三角形の面積比 なかけんの数学ノート
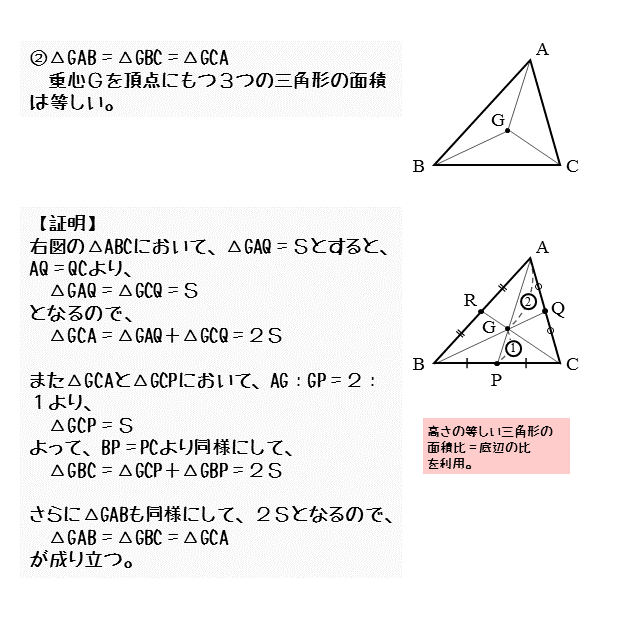



図形の性質 重心について 日々是鍛錬 ひびこれたんれん




平面図形をマスター 三角形の面積比 応用編その3




3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




相似 台形と面積比の問題を徹底解説 数スタ
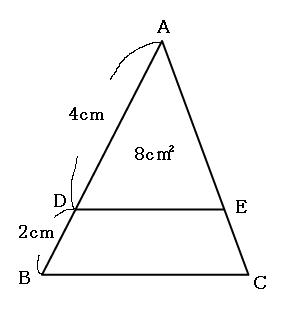



相似比と面積比と体積比の関係を解説 公式を使って面積や体積を求めよう



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋



Newみんなの算数講座86 三角形を全部見てはいけない 中学受験の算数知恵宝庫



長さ比から面積比の求め方 算数解法の極意



長方形内にある三角形の面積比 シリーズ 木を見て森を見ずにあらず 273回解答 解説 ブリコラージュ




勉強しよう数学解答集 三角形の3頂点のベクトルの張る三角形の面積比の公式




辺の比と面積比問題 考え方1 Youtube




数 A チェバ メネラウスの定理と三角形の面積比は線分の比を活用しよう 岡山医学科進学塾のブログ




よく出る台形の面積比 算数 過去問で基本を鍛える 12 勉強法のバイブル 帝都大学へのビジョン



Mathematics 相似 4 面積と比 面積比は となりあった三角形で求める 働きアリ




三角形の面積 三角比 Geogebra




数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生



三角形の辺と面積の比 父ちゃんが教えたるっ




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



相似な図形 面積の比 苦手な数学を簡単に



辺の比と面積比 等角三角形 富士山型 Next Stageのブログ



1




三角形の面積比 数学の偏差値を上げて合格を目指す




平面図形をマスター 三角形の面積比 応用編その3
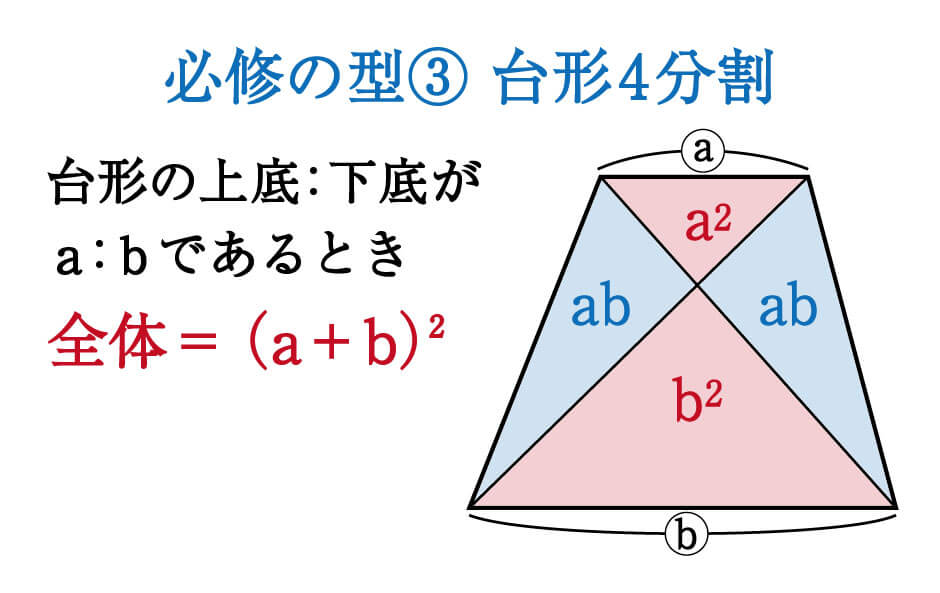



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
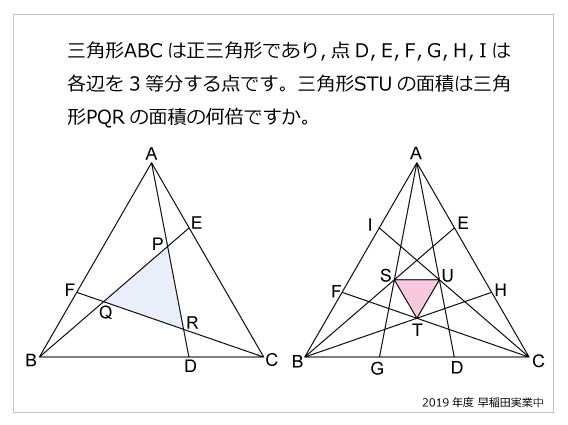



今年の1問 19年早稲田実業中 正三角形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦




平面図形をマスター 三角形の面積比 応用編その2




高校入試対策数学 面積比に関する対策問題 Pikuu



三角形の辺と面積の比 父ちゃんが教えたるっ




大至急です 相似 面積比の問題です Clear
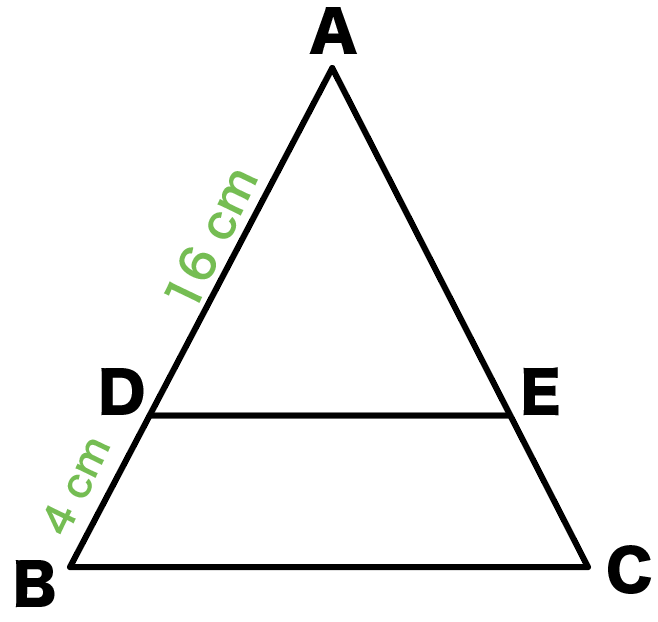



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく



1




中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su
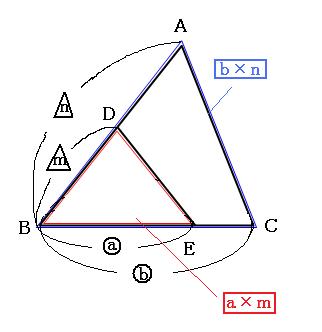



面積と辺の比の関係を解説 図形の面積と辺の比の関係はテントやドリルで面積を求める




数学 三角形の辺と面積の比について 2つの考え方をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生




高校数学a 三角形の面積比 等高 等底 等角 受験の月




三角比を使って三角形の面積を求める方法 数学i By Okボーイ マナペディア
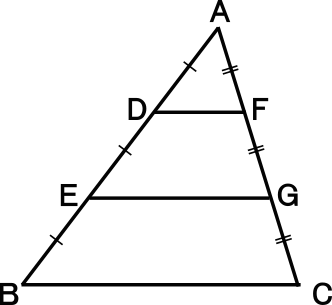



中学3年数学練習問題 相似な平面図形の面積の比 図形と相似




面積比 2つの三角形で高さが同じときの面積比 身勝手な主張




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




三角形の面積比と相似比 チーム エン




中学受験算数 面積比の達人 仮 Yell Books みかん 本 通販 Amazon




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学




平面図形の苦手を解消 三角形の面積比 基本編



1




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
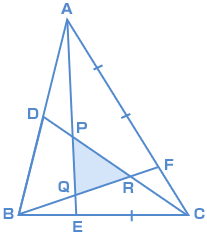



算数 平面図形と比 1 中学受験 ベネッセ教育情報サイト




三角形で面積比と底辺の比の関係は 平面図形分野の頻出問題を考える みみずく戦略室



面積比 長さ比 これが中学入試に出た図形問題




ベクトル方程式による面積比の問題と解き方
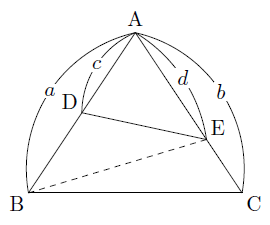



1角共有の三角形の面積比 まなびの学園



図形 面積比の応用 三角形の面積比 名古屋市北区の学習塾は思考力を育む 泰成スクール



3



面積比とは 1分でわかる意味 公式と求め方 問題 三角形と四角形の関係




図形の面積比 知っている人は5秒以内には解ける面積比の裏技 Youtube




小学6年生 算数 10月 辺の比と面積の比 速さ 1 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ
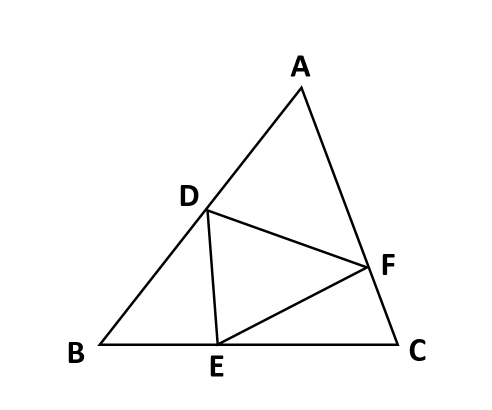



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ




数学 入試で差がつく 線分比と面積比の関係をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生




メネラウス型 辺の比と面積比 Nextstage Warehouse



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ




相似じゃない三角形の面積比の求め方がよく分かりません Clear




中学校数学 証明のコツ 入試で差がつく 面積の比 体積の比 を得意にできる教材
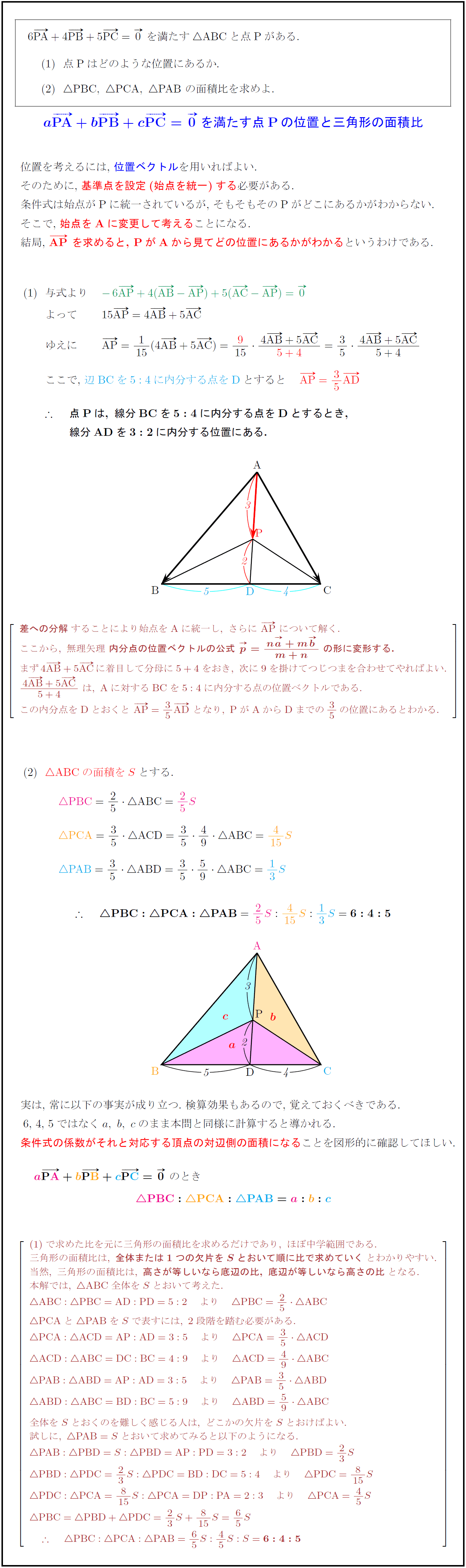



高校数学b Apa Bpb Cpc 0を満たす点pの位置と三角形の面積比 受験の月



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




辺の比と面積比 基本編 Youtube
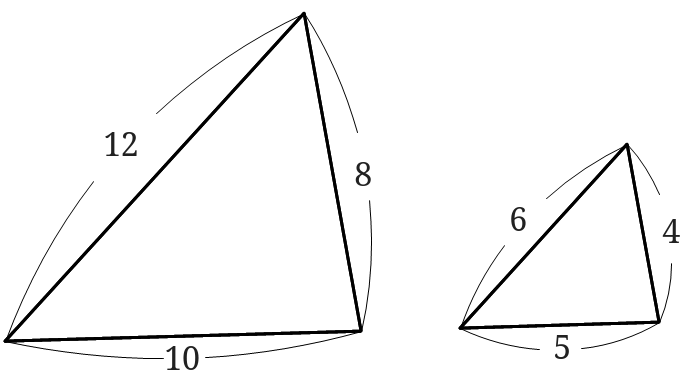



相似な図形の面積比と三角形の辺の比から求める面積比 まぜこぜ情報局




平面図形をマスター 三角形の面積比 応用編その3
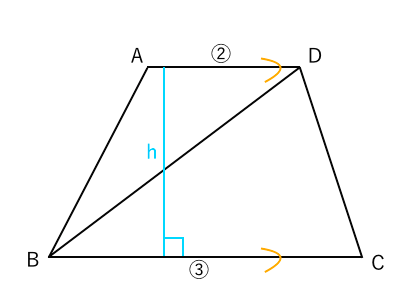



簡単に面積が何倍か求められる 使える編 苦手な数学を簡単に



数学の質問です 図のように 1つの角を共有する2つの三角形の Yahoo 知恵袋




平面図形をマスター 三角形の面積比 応用編その3



数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三角形の面積と面積比 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc




平面図形の苦手を解消 三角形の面積比 基本編



面積比 長さ比 中学受験ー算数解き方ポータル



中学受験 算数数学が苦手な子専門のプロ家庭教師みかん先生




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




相似の面積比を求める問題 上級編 Youtube



平面図形 辺の比と面積の比 前田昌宏の中学受験が楽しくなる算数塾



数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



第5章 面積の比と体積の比 台形の相似比と面積比 中学生




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ




三角形の面積比にまつわる公式たち 高校数学の美しい物語



Mathematics 相似 4 面積と比 面積比は となりあった三角形で求める 働きアリ The 2nd



8 面積比の6パターン って 中学受験ドクター Youtube



三角形の面積 辺の比



第5章21 面積の比と体積の比 平方四辺形の相似比と面積比 フロントエンドなブログ


