第一冊 2~3 直角坐標平面 33 直角座標平面 S 一年 班 號 姓名 分數 1 已知 A ( 3,2 ),B ( 6,1 ),若 P 在 上,且 : = 5 : 2 ,求 P 點坐標。 ( 36/7 , 1/7 ),( 8,3 ) 2 已知 A ( 5 ,9 ),B (3,1 ), C ( 4 ,2 ), 求 ABC 的重心坐標。 ( 2,4 ) 3 如右圖直線 L 1,L 2, L 3,L 4 的斜率分別為 m 1, m 2 6( )坐標平面上,直線方程式 16x y=1 與兩軸所圍成的三角形面積為多少平方單 16 位?(A);(B) (D)16。 7 (5)在坐標平面上有一隻螞蟻牠沿著直線工作直線爬行,一分鐘後牠停在(1,1),又 經過5分鐘後,牠停在(0,4),請問L的直線方程式為何?軌跡を求める手順 1求める軌跡上の任意の点の座標を ( , ) などで表し、与えられた条件を座標の間の関係式で表す。 2軌跡の方程式を導き、その方程式の表す図形を求める。

三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく
円 三角形 方程式
円 三角形 方程式-慣性モーメント:一般論 慣性モーメントはいくつあるのか?無数? 1)重心を通らない回転軸の i は,重心を通根據外角定理:三角形任一外角等於另外兩個內角之和, ∠ aob=∠apb∠b=2∠apb。 圓心角∠ aob 所對的弧為



名師課輔網 直線平分三角形面積求方程式
電電對於三角形與方程式非常著迷,只要是三角形,不論是去大福買的三明治還是夏季大三角,他都非常喜歡,而且有股想把它們的面積算出來的衝動。 有一三角形 $ \bigtriangleup $ 其三邊長為 $ x^3 bx^2 cx d = 0 $ 的三個根 其面積為 $ \sqrt{n} $ 求 $ n $鈍交角分角線方程式可以表為 = (二)如果兩法向量夾角為鈍角時, < 0, 兩直線銳角所在區域為同號區,所以 銳交角分角線方程式可以表為 = 兩直線鈍角所在區域為異號區 鈍交角分角線方程式可以表為 =- ()( () () () () ) ()(31) 管流方程式 (311) 管流方程式簡化 222 22 2x u u u u P uuu uv w g txyz x xyz 穩態流: 0 u t 假設一維流:v 0,w 0 磨擦力主要來自側向的速度梯度: 22 2 22 2 1 uu u u r x yzrr r
1 基礎量子化学 11年4月~8月 7月1日第11回 11章分子構造 分子軌道法 11・6ヒュッケル法 担当教員 福井大学大学院工学研究科生物応用化学専攻准教授將方程式a(x−x0)b(y−y0)c(z−z0)=0 化簡可得axbyczd=0的方程式。 我們將 ax by cz d =0稱為一般式。 一般式 ax by cz d =0的法向量為 n =( a , b , c )影片:例題直角三角形面積的計算題 1,數學 > 主題式 > 國小 > 空間與形狀 > 平面圖形 > 五年級三角形與四邊形的面積。源自於:均一教育平台 願 每個孩子都成為終身學習者,成就自己的未來。
第12 章空間幾何 121 向量的叉積 (3) 若θ 是a 與b 之間的夾角(0 • θ • π), 則 ja£bj = jajjbjsinθ。 (4) a£b 的長度是a 及 b 所張成之平行四邊形的面積。 (5) 若a,b 6= 0, 則 a 與b 平行的充要條件為a£b = 0。 (6) 令 a,b 為空間中的非零向量, 若a,b 不平行, 則 a,b 決定一平面E。令該平面的單位法向量三角形 A 為銳角三角形 三角形 A 為直角三角形 三角形 A 為鈍角三角形 有兩實根 重根 無實根 (二)a、b、c為直角三角形 A 的三邊長,以下方程式皆能形成重根 (ca)x22bx(ca)=0 x= − (ca)x22bx(ca)=0 x= (表一資料來源 李承暉、連珮妤(18)。當三角形遇見方程式。三角函數,是人們用來表示三角形上邊長與邊長之間關係的函數。當我們觀察一個直角三角形時,我們可以將各個函數定義作如下:$$ sin(\theta) = \frac{對邊}{斜邊} ,cos(\theta) = \frac{臨邊}{斜邊} $$$$ csc(\theta) = \frac{斜邊}{對邊} ,sec(\theta) = \frac{斜邊}{臨邊} $$$$ tan(\theta) = \frac{對邊}{臨邊} ,cot(\theta) = \frac



干货分享 三角形中的直线方程 中线 高 角分线



初中数学 利用相似三角形 构造一元二次方程式 网易视频
範例12 ( )三直線x ( y ( 9 ( 0﹐x ( 2y ( 0及3x ( y ( 7 ( 0圍成一三角形﹐設此三角形外 接圓的方程式為x2 ( y2 ( ax ( by ( c ( 0﹐則 (1)此三角形的三頂點為(2 , ( 1)﹐(6 , ( 3)﹐( ( 1 , ( 10) (2)a ( b ( 8 (3)2a ( b ( (4)外接圓圓心的坐標為(2 , ( 6) (5)a2 ( b2 ( 4c ( 100﹒第7章 有限要素法 有限要素法(finite element method ,略してFEM あるいはFEM)は,現在工学の多種 多様な問題の数値解析,シミュレーション法として多用されており,計算力学を支える有力Free online apps bundle from GeoGebra get graphing, geometry, algebra, 3D, statistics, probability, all in one tool!




3种方法来计算三角形的周长




数学方程式公式模板元素素材下载 正版素材 摄图网
若設圓心O(h,k),半徑為r,則此圓的方程式為(x−h)2(y−k)2=r2。 推導:設P( x , y )為圓上的點, PO = r ⇔ ( x − h ) 2 ( y − k ) 2 = r小三 三角形之間的關係 認識不同種類三角形之間的關係 認識三角形任意兩邊長度之和大於第三邊的長度 新增 小三 棒形圖 (一) 一格代表 1、2 和 5 個單位的棒形圖円周角の定理の証明|図で分かりやすく解説 5月 21, 管理人 数学FUN 円周角の定理は、1つの弧に対する円周角・中心角に関する定理です。 円周角の定理 1つの弧に対する円周角は等しい その円周角はその弧に対する中心角の半分である 中学校数学




數學 康軒版




勞厄方程式 维基百科 自由的百科全书
2) 型的直角三角形。 於是當我們看到2x 3y = 6 時,我們可以先找一個點滿足2x 3y = 6,例如:(3;0),然後 由 2x3y !{ \left( \sin ( x ) \right) }^{ 2 } \cdot \left( { \left( \cot ( x ) \right) }^{ 2 } 1 \right) sin (x)) 2 ⋅ ((cot (x)) 2 1)範例 4 在坐標平面上畫出下列各二元一次方程式的圖形 (1)x=2 解 因為x=2與x0×y=2 是相同的方程式 所以先找出任意相異兩組解 將此兩點 ( ,0) 、 ( ,1) 畫在 坐標平面上,並畫出通過這兩點 的直線,此直線即為 x=2 的圖形。 (2)2y3=0



1




外接圓 维基百科 自由的百科全书
平行四辺形の面積が (底辺)×(高さ) で求めれることを思い出してもらうと 三角形の面積公式は、このように考えることができますね。 三角形の面積を求めるためには 一旦、平行四辺形の面積を求め それを半分にしている。 だから、2で割る必要「已知三邊直線方程式之三角形面積公式」 的另一種證法 PDF 檔案知三角形三邊所在直線方程式之面積公式」),立刻引起筆者的興趣。 這篇文章最後得到 一個相當漂亮的公式,由直線方程式的係數和二階,三階行列式組合而成,形式簡單對 稱,讓筆者留下非常深刻的印象,久久難以忘懷。聯立方程式的圖形例題講解 三直線圍成三角形 直角坐標與二元一次方程式的圖形 (七下) 平面上的點 平面上的點例題講解 寫出坐標 平面上的點例題講解 畫出點的位置 平面上的點例題講解 點到軸的距離 象限 象限例題講解 判斷象限 (1)




求這兩題的解釋謝謝 Clear



聯立方程式的圖形例題講解 三直線圍成三角形 直角坐標與二元一次方程式的圖形 七下 發現學習的美麗新世界
16_ (1257) 三角形の方程式について 船橋啓明高等学校新堀弘騏 平面上の直線や円の方程式は,かなり以前に見つかっており,よく,使われもして三角形之三邊所定直線方程式為, , , 若與三角形有交點, 求m的範圍 類題 設A ( 2, 3 ), B ( 4, 0 ), 若線段與直線相交, 則k之範圍為 己 對稱點與極值問題之求法 1 對稱: 若點在直線L上或直線L為線段的垂直平分線, 則稱點與 對於直線L為對稱 三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




傲览千古on Twitter 描述曲线和曲面的代数方程式描述实心直角三角面描述直角三角形描述阴空心直角三角面
三角形的內心、重心、垂心 、外心、外心圓半徑及圓方程 程式是參考網友 yuen 的程式編寫。 已知三角形三頂點的坐標,程式可計算三角形的內心、重心 、垂心、外心、外心圓半徑及圓方程。第10 章參數方程與極座標 101 參數方程式 註 1012 若一函數y = f(x) 可將其參數化為x = t, y = f(t)。則其反函數可參數化為 x = f(t), y = t。 例 1013 討論以下曲線 (a) x = acost, y = asint, t 2 0,2π。 (b) x = acost, y = asint, t 2 0,π。 (c) x = acost, y = asint, t 從π 到 0。 (d) x = sin2t, y = cos2t、t 2 0,2π。 例 1014




工作三角形公式幂方程科学公式png图片素材免费下载 图片编号 Png素材网




3 1 平面方程式




基測數學 91v1 單選23 矩形與三角形面積 評量專區 均一教育平台
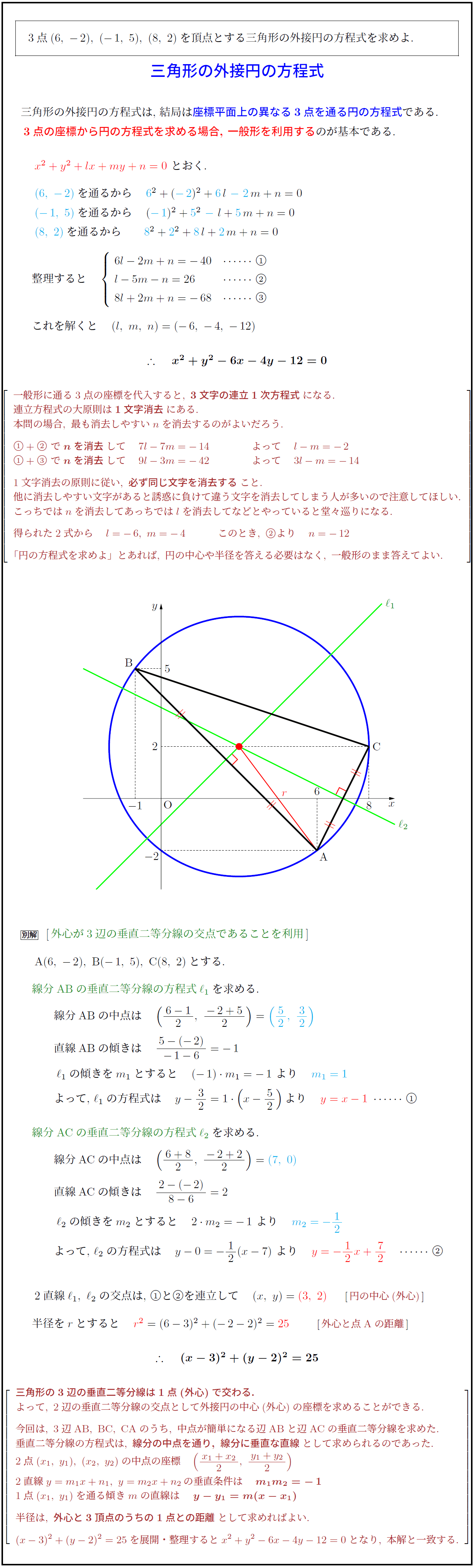



高校数学 三角形の外接円の方程式 受験の月



2次方程式 三角形と動点の文章問題 勉強ナビゲーター



用solidworks方程式建模的正三角环 修改参数后图形会自动变化 钣金加工




直線方程式應用 信欣茗數學園地 隨意窩xuite日誌




高校数学 三角形の内接円の方程式 受験の月



1




直角三角形 翰林雲端學院




如何用斜率判斷是不是直角3角形 Clear




常用的放大器配置设计方程式 讨论 放大器专区 Engineerzone




三角形摩尔浓度公式计算 三角形png图片素材免费下载 图片编号 Png素材网




三角形面積公式sin 三角形面積公式 Duph




直線方程式



三角的数学方程式矢量图png图片免费下载 素材7xsqgawju 新图网



三角形的外接圆 知乎




数学ii 図形と方程式 2 2 三角形の形状 Youtube



名師課輔網 二元一次圖形 第6題




New Ios App 中1計算問題方程式 Manabu Narawa Tech Company Logos Company Logo Ibm Logo
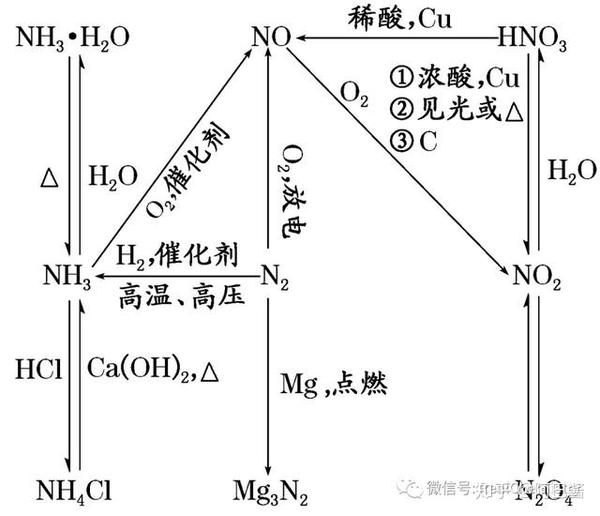



雷电作用固氮方程式 雷电作用方程式 雷电固氮的化学方程式




03三角形的三边关系三角形 1 初中数学初一 Youtube



名師課輔網 直線平分三角形面積求方程式
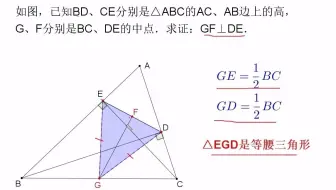



初中数学 直角三角形中 利用中点和勾股定理 构造方程式求解 哔哩哔哩 Bilibili




三角形中的直线方程 参考网




隨筆誌 設直線l過點 2 3 且在第四象限與兩座標軸所圍成的三角形面積最小 求直線l的方程式



方程式图片素材 免费方程式png设计图片大全 图精灵



ようこそアンパンの部屋へ 三角形の面積や長さの公式




数学方程式设计图 Psd分层素材 Psd分层素材 设计图库 昵图网nipic Com



梯形怎么画4个三角形 搜狗图片搜索




三角形 21 直角三角形面積的基本計算題 Youtube



Ae模板数学代数方程式计算公式标识揭示math Formulas Logo Reveal V2 柚皮cg资源网站




高二數學空間中的平面方程式 急 信欣茗數學園地 隨意窩xuite日誌




中一年級試卷和答案17 Pdf




数学公式 绿色学校黑板数学公式 手写科学数学方程式理论向量例证 插画包括有选件类 图画




高二數學 平面方程式 信欣茗數學園地 隨意窩xuite日誌



干货分享 三角形中的直线方程 中线 高 角分线



手绘数学矢量无缝图案 手写代数公式 方程式和几何图形在白皮书上库存矢量图 免版税



展示数学美丽和力量的11个方程式 你最喜欢哪一个 快资讯




3种方法来计算三角形的周长



数学矢量无缝模式与手写的数学公式 计算 方程式 您可以使用任何颜色的背景库存矢量图 免版税



泵的基本方程式 三联泵业股份有限公司



解一元二次方程式之應用問題合理性 Live 多媒體數學觀念典online




正偶邊形與正偶圓弧的方程式 臺灣網路科教館




双摆运动三角形方程png图片素材免费下载 图片编号 Png素材网




科学史上最美丽最重要的9个数学方程式 哔哩哔哩




4 直線方程式與二元一次不等式 乙




S 5 上學期考試 Q42 直線方程 三角形面積 Youtube




一个小三角形表示 化学方程式的一个小三角形是什么意思 三人行教育网 Www 3rxing Org
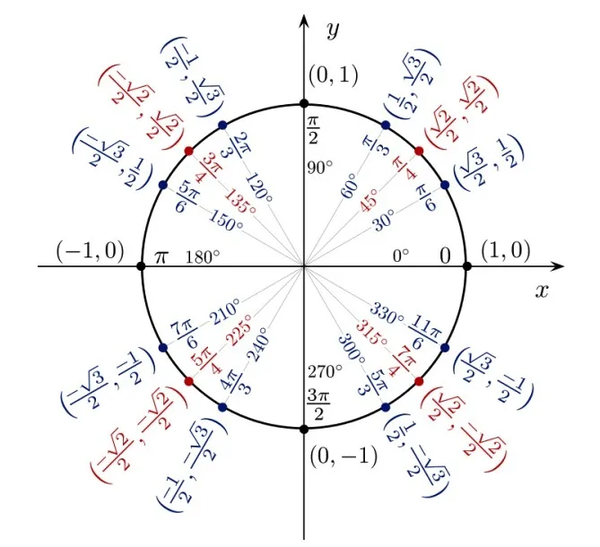



数学老师喊麦三角函数刷屏 Sat数学三角函数了解一下 知乎




傲览千古a Twitter 如果是在 平面拓扑几何学 中 该方程式 X Y R 可描述多种不同的曲线 即使它们是那种 不同胚 的一维曲线 比如 它可描述一条直线段 或者一个圆 或者一个直角三角形



有問有答




Fvazlexfd5rtpm




例題 一元二次應用題 直角三角形 Youtube



1




Watlow 三角形和y 型电路方程式




今日から使えるロジカルシンキング 成功者は鍛えてる 一見 三角形の問題 を 連立方程式の問題 と見破る力 1 2ページ Sankeibiz サンケイビズ 自分を磨く経済情報サイト




三角形の内接円の方程式の求め方 数学の偏差値を上げて合格を目指す




如何通过三角形的顶点坐标找到边的方程 数学21



方程式 万图壁纸网




宇宙數學教室 三角形三心綜合題 善用圓切線性質 避過解困難方程式



三角爱学的方程式png搜索网 精选免抠素材 透明png图片分享下载 Pngss Com



三角爱学的方程式免抠素材免费下载 觅元素51yuansu Com



三角手绘类方程式免抠素材免费下载 觅元素51yuansu Com




求這兩題的解釋謝謝 Clear




确定斜边的长度 建议 August 21




Microsoft Math 轻松解决复杂数学问题 生活方式 21



初中数学方程式大全你需要的公式都在这里 初三网



中國人最早發現這個三角形



正三角形外接圆算法 西瓜视频搜索




三角的数学方程式png图片素材免费下载 图片编号yrkenbdq Pngbag素材网




11等边三角形面积公式勾股定理初中数学初二 Youtube




翻轉學習影片 高中 數學 三角形邊上高的直線方程式
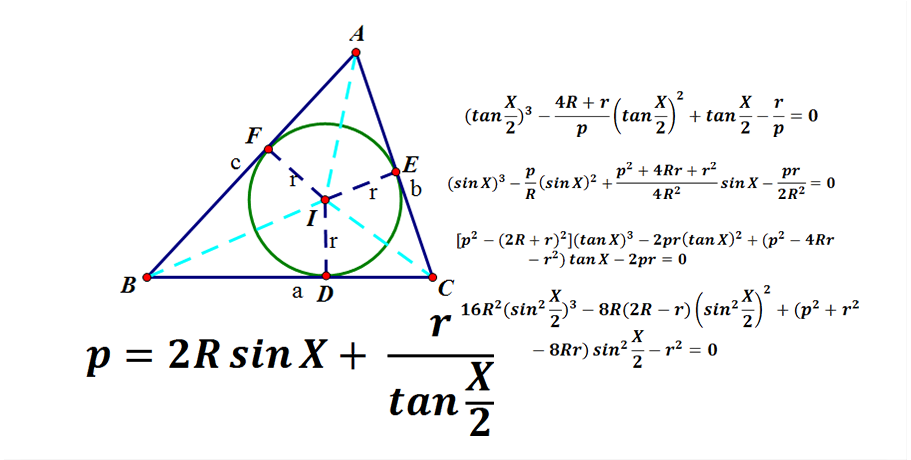



三角形与一元三次方程 知乎
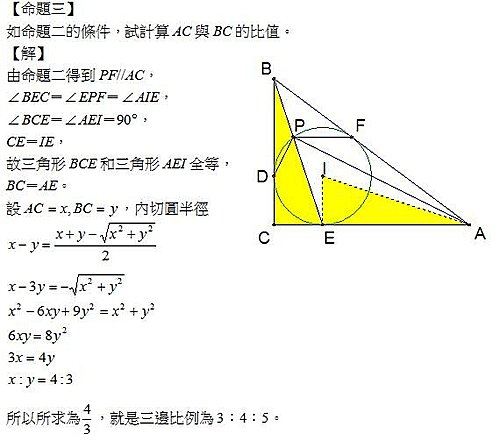



345直角三角形的性質 老王的夢田 痞客邦




长方形手绘类方程式png图片素材免费下载 图片编号qpwkwvgy Pngbag素材网
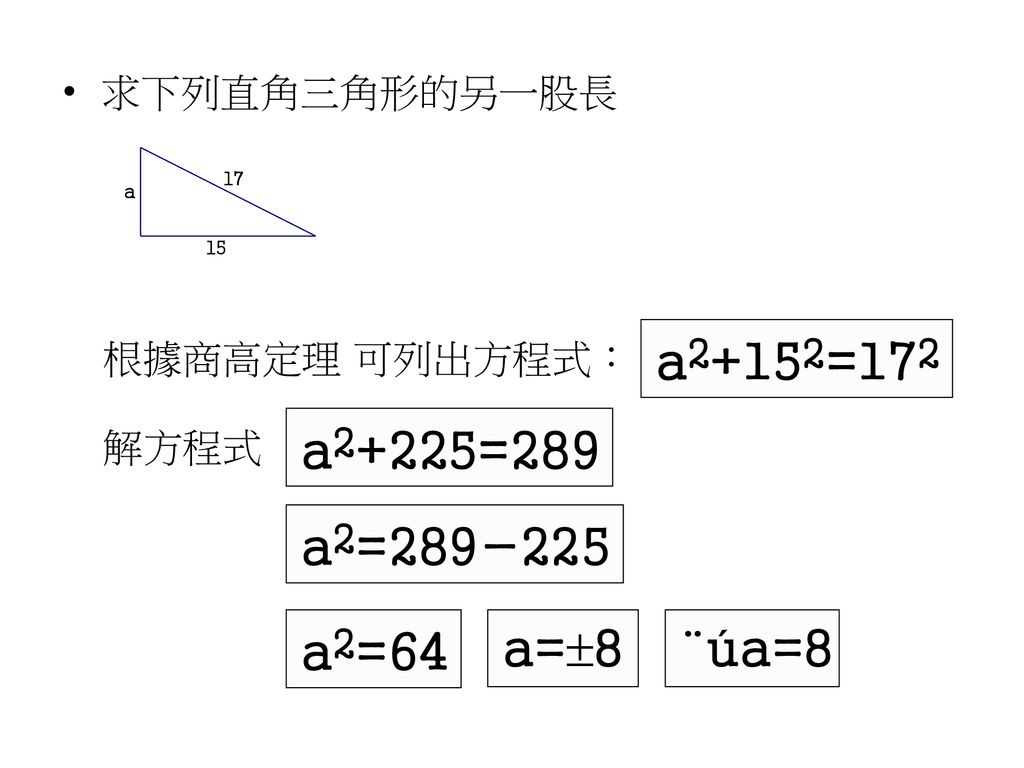



有一個長方形 它的長是6公分 寬是8公分 問它的對角線長是多少公分 Ppt Download



启智学术等边三角形方程式 东奇庚 新浪博客



1




佰俐b 由申甲國一數學一元一次方程式一 二 二元一次聯立方程式 三角形的基本性質 國二數學圖形概念 54本 露天拍賣



物理動畫 數學 等差數列 1



数学方程式草稿纸学习元素素材下载 正版素材 摄图网




基測數學 90v2 單選30 直線方程式與兩軸圍成的面積 評量專區 均一教育平台




一级方程式挂绳



名師課輔網 直線方程式及圖形 等腰三角形內心




巧解初中數學方程式 每日頭條




3 1 平面方程式
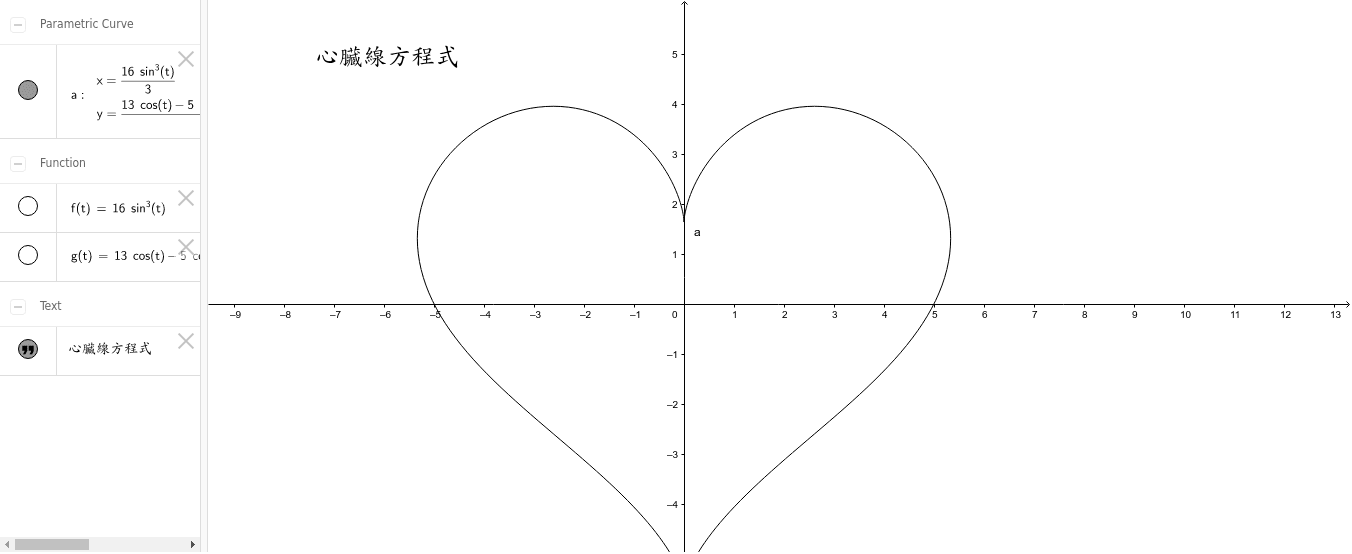



心臟線方程式 Geogebra




如何通过三角形的顶点坐标找到边的方程 数学21




Amazon Com 教養方程式 你的角色 決定孩子如何出色 Traditional Chinese Edition Ebook 隆納 弗格森 Ronald F Ferguson 塔莎 羅伯森 Tatsha Robertson 王素蓮 Kindle Store




在pages中使用方程式时 如何使平方根不那么 高 21




等角三角形 翰林雲端學院


