鋭角三角形の特徴とタイプ の 三角形三角形 3つの内角が鋭角の角です。 つまり、これらの各角度の測定値は90度未満です。 直角を持たないので、ピタゴラスの定理はこの幾何学的図形に対して満たされていないことがわかります。 したがって、その三角形(さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。 その3点を三角形の頂点、3つの線分を三角形の辺という。 目次 1 記法・定義 11 三角形を成り立たせる3辺 (三角形の成立条件)それら以外の三角形 これらの特徴も 覚えているはずですが、 この特徴 今回は中2数学で習う三角形の分類、鋭角三角形・鈍角三角形・直角三角形の違いに
直角三角形と証明 中学2年 数学クラブ
鋭角三角形 三角形 種類
鋭角三角形 三角形 種類- 問題文 2 次元平面上の N 個の点が与えられます。i 番目の点の座標は (x_i, y_i) です。 ただし、このうちのどの 3 点も同一直線上にありません。 N 点のうち 3 点を選ぶことによってこの 3 点を頂点とした三角形を作ることを考えます。 三角形は全部で N * (N 1) * (N 2) / 6 個できます。三角形 四角形 三角形の内角の和 𝟖 ° 平行四辺形 定義2組の対辺がそれぞれ平行な四角形 三角形の外角は、それととなり合わない 2つの内角の和に等しい 2組の 対辺はそれぞれ等しい 三角形の合同条件① 3組の辺がそれぞれ等しい




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強
An Acute Triangle(鋭角三角形) 鋭角三角形は、an acute triangleと言います。 acuteは、鋭いという意味です。 例えば、an acute angleは、鋭角、90°未満の角度です(角度に関する英語表現はこちら)。 An acute triangle is a triangle with all three angles acute (筆者訳)鋭角三角形 三角形の 3 つの内角の大きさに注目して、すべての角が鋭角である三角形を 鋭角三角形 (図 2)、1 つの角が直角である三角形を 直角三角形 (図 4)、1 つの角が鈍角である三角形を 鈍角三角形 (図 3)という。直角三角形による三角比の定義 ある鋭角に対して、足し合わせると直角となるような角のことを余角(英:complementary angle, coangle)という。 実際、三角比は6種類あり、これは次回の記事
直角三角形の中に、二等辺三角形を描く 三角定規は二種類の直角三角形で作ってあります。 これは正三角形と正方形を半分にして作ったものです。 正方形からは直角二等辺三角形、正三角形からは30・60度の直角三角形ができますが、 三角形の形状の分かれ目 (その二) 数学 本記事では、三辺のうち二辺の長さが既知で残りの一辺の長さが未知である三角形の形状が鋭角三角形・直角三角形・鈍角三角形のいずれになるかについて考えます。 長さが既知である二辺のうち長い方をa、短い方正九角形 正九角形においては、中心角と外角は40 °で、内角は140°となる。 一辺の長さがaの正九角形の面積Sは、 = となる。 (/) を平方根と立方根で表すと 、 = = = = = 正九角形は定規とコンパスによる作図が不可能な図形である。 正九角形の頂点を二つおきに線で結ぶと正三角形が
三角形 三角形の概要 ナビゲーションに移動検索に移動この項目では、図形について説明しています。記号文字については「三角 (記号)」をご覧ください。 三角形目次1 記法・定義11 三角形を成り立たせる3辺 (三角形の成立条三角形は全部で5種類あります。 四角形はどうでしょうか。三角形の種類 小学4年は三角形を 4つ覚えているはずです。 二等辺三角形; 多角形 分類 いくつか異なる種類の多角形辺の数多角形は第一義的にその辺の数でできる。n 個の辺を持つ多角形は n角形あるいは n辺形と呼ぶ。凸性・凹性多角形をその凸性あるいは凹性によって特徴付けること




質問 数学a 図形 三角形に外接円が必ず存在する理由 オンライン無料塾 ターンナップ
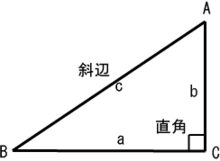



直角三角形 Wikipedia
Contents1 三角形の内角11 問題2 三角形の外角21 三角形の1つの外角は、その隣にない2つの内角の和と等しい22 外角は対頂角になっている23 三角形の内角と外角のまとめ図24 問題3 三角形の種類 「この中に三角形はいくつある?」との問題が意鋭角三角形 (えいかくさんかっけい、 英 acute‐angled triangle )は、 三角形 の一種で、すべての角が 直角 (90 ° =π/2 rad) よりも小さい 図形 である。 三角形の種類 三角形は内角の大きさによって,$3$ 種類に分けられます. すべての内角が $90°$ 未満のとき,鋭角三角形と言います. 一つの内角がちょうど $90°$ のとき,直角三角形と言います. 一つの内角が $90°$ より大きいとき,鈍角三角形と言います.




鋭角三角形 Wikipedia




中学2年生の数学 証明 二等辺三角形と直角三角形 塾講師が数学をやりmath
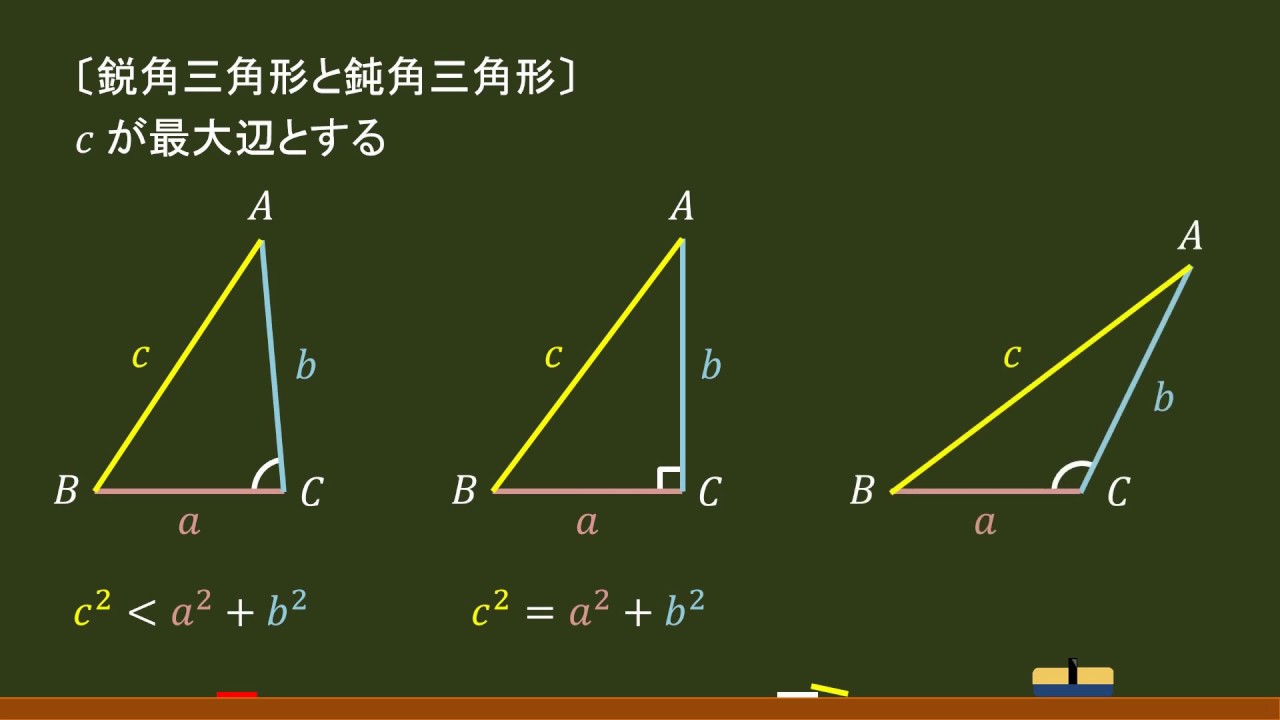
上野竜生です。3辺の長さが与えられたとき三角形が成立するのか,成立するなら直角三角形か鋭角三角形か鈍角三角形かを判定することについて考えましょう。 言葉の意味 鋭角三角形:すべての角が鋭角(90°未満)である三角形 直角 三角形には、いくつかの種類があるのは小学校で習いましたが、鋭角三角形や鈍角三角形などという表現は忘れている方もいらっしゃるかも知れませんね? ちなみに、英語で辺は「sides」、角は「angle」、そして直角のことを「right angle」、鋭角は「acute angle鋭角三角形となる面積:鈍角三角形となる面積 2 2 =3:1 したがって、鋭角三角形となる確率は、3/4。 鈍角三角形となる確率は、1/4。 (3/4+1/4=1。)以上です。 alephさんの解答と逆になってしまいました。




三角形の面積
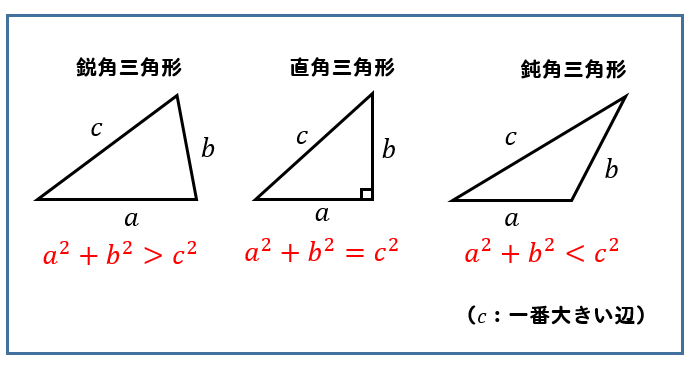



鋭角 鈍角三角形 三平方の定理を使って見分ける方法を解説 数スタ
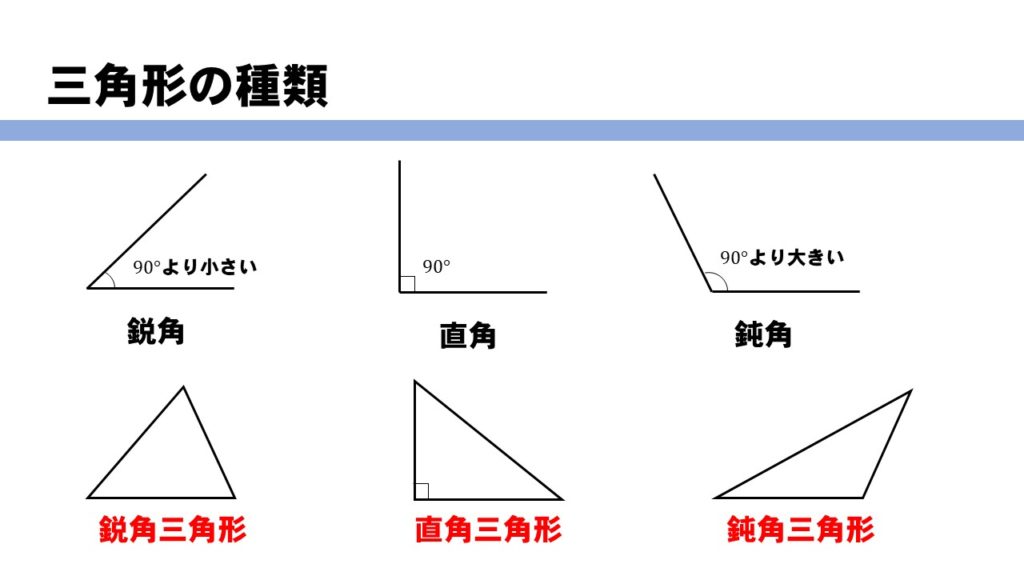
中2数学「三角形の内角と外角の定期テスト過去問分析問題」です。 三角形 三角形の内角の性質三角形の内角の和は180°です。 三角形の外角の性質三角形の1つの外角は、そのとなりにない2つの内角の和に等しい。 鋭角・鈍角 鋭角0°よ三角形の形状判定 (鋭角・直角・鈍角) の対応動作環境 ソフト名: 三角形の形状判定 (鋭角・直角・鈍角) 動作OS: Windows 10/8/7/Vista/XP 機種: IBMPC x64 種類: シェアウェア :100円三角形について、 1番大きい角度が 90 ∘ より小さい→ 鋭角三角形 1番大きい角度が 90 ∘ ぴったり→ 直角三角形 1番大きい角度が 90 ∘ より大きい→ 鈍角三角形




全くわかりません 答え教えてください Clear



鋭角三角形とは 1分でわかる意味 条件 直角三角形 鈍角三角形との違い
鋭い三角形には3つの内接する四角形があります。 各正方形は、三角形の側面の一部と一致します。 正方形の他の2つの頂点は、鋭角三角形の残りの2つの辺にあります。 オイラー線が片側に平行な三角形は鋭角三角形です。 今回は中2数学で習う三角形の分類、鋭角三角形・鈍角三角形・直角三角形の違いについて勉強したいと思います。 鋭角とは? 直角とは? 鈍角とは? 三角形の分類 鋭角三角形 直角三角形 鈍角三角形 三角形の分類に関する問題 問題① 問題② まずはじめに鋭角、鈍角、直角という言葉の意味 鋭角三角形は、すべての角度が90°未満の三角形として定義されます。言い換えれば、鋭角三角形のすべての角度は鋭角です。 急性三角形の特性 すべての正三角形は鋭い三角形です。正三角形には、同じ長さの3つの辺と、60°の3つの等しい角度があります。
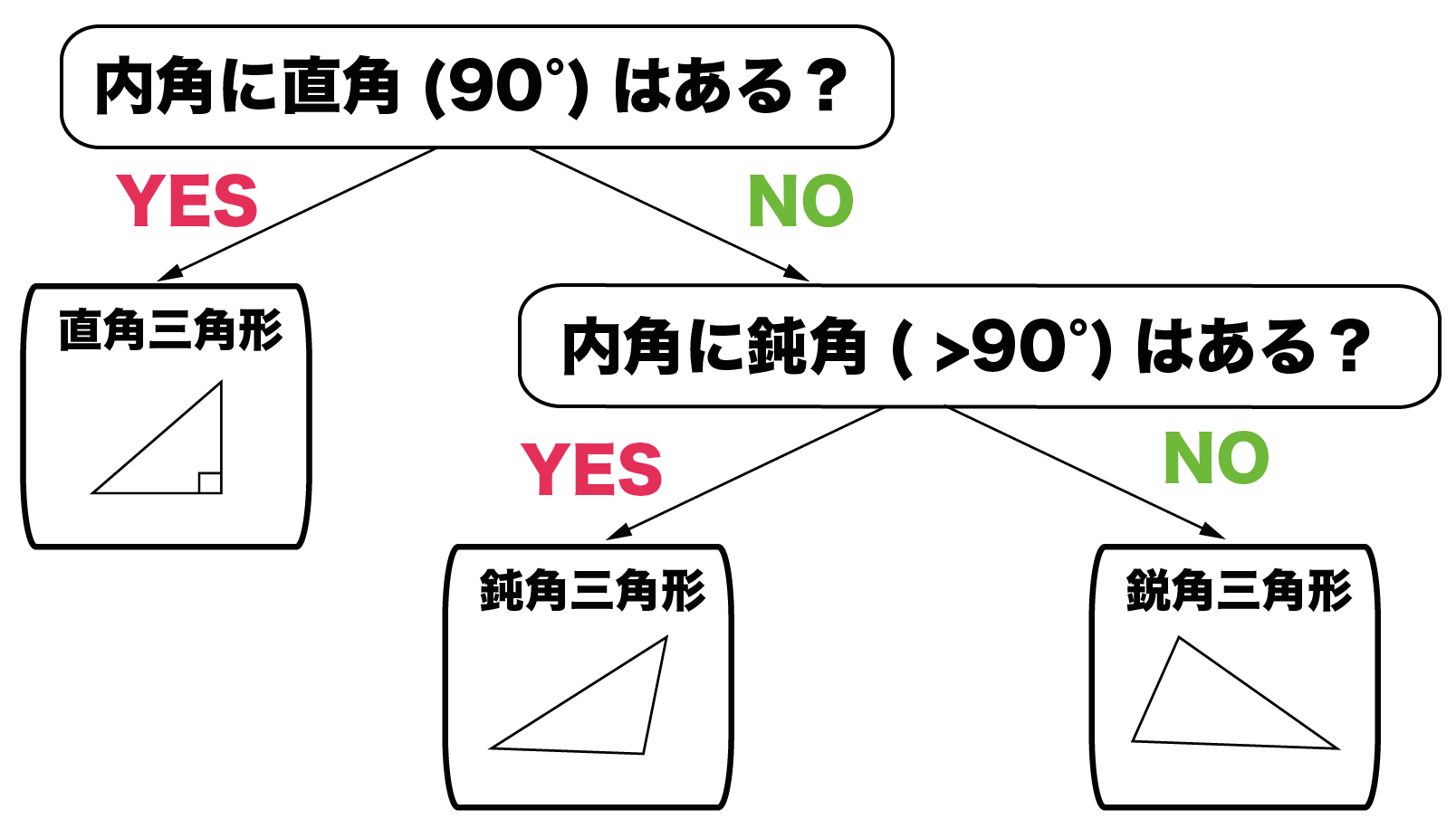



鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく




正三角形 Wikiwand
三角形の合同条件 3組の辺が、それぞれ等しい 2組の辺とその間の角が、それぞれ等しい 1組の辺とその両端の角が、それぞれ等しい 合同な図形の対応する 線分の長さ 角の大きさ はそれぞれ等しくなります 先生によって<三角形の種類> ・正三角形 一番メジャーな三角形。内角が全て60°で成り立っている、育ちの良い三角形。 ・直角三角形 ひとつの角が90°の三角形。ピタゴラスの定理(a2b2=c2)はあまりにも有名。 三角形界のダルビッシュ的存在。 ・二等辺三角形算zan 5種類全部覚えるのが目標ですね。 これが 正三角形(せいさんかくけい) です。 正三角形とは 3つの辺の長さが等しく、3つの角の大きさが等しい形 のことです。




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強




中2数学 多角形の角 内角 外角の性質 鋭角 鈍角 Youtube
1 第1次 三角形と四角形 辺の数に着目すると、はっきりと ・辺の数に着目して、図形を「三角形」と「その他」 仲間分けできるね。 に分類し、三角形の特徴を言葉でまとめる。 三角形は、おにぎりのように、3 本の直線で囲まれた形だよ。(57)要約 課題 鋭角特徴を再現した三角形メッシュを生成す る。 解決手段 与えられた点群の中からランダムに選択 した点の近傍点を求め(S2,S3)、ドロネ三角形分 割処理により局所メッシュを生成する(S4)。得られ た局所メッシュに対し、特徴復元とスムーズネス向上の ため




正三角形 直角三角形 の韓国語は 三角形の種類や特徴を表現してみよう 気になるkorean
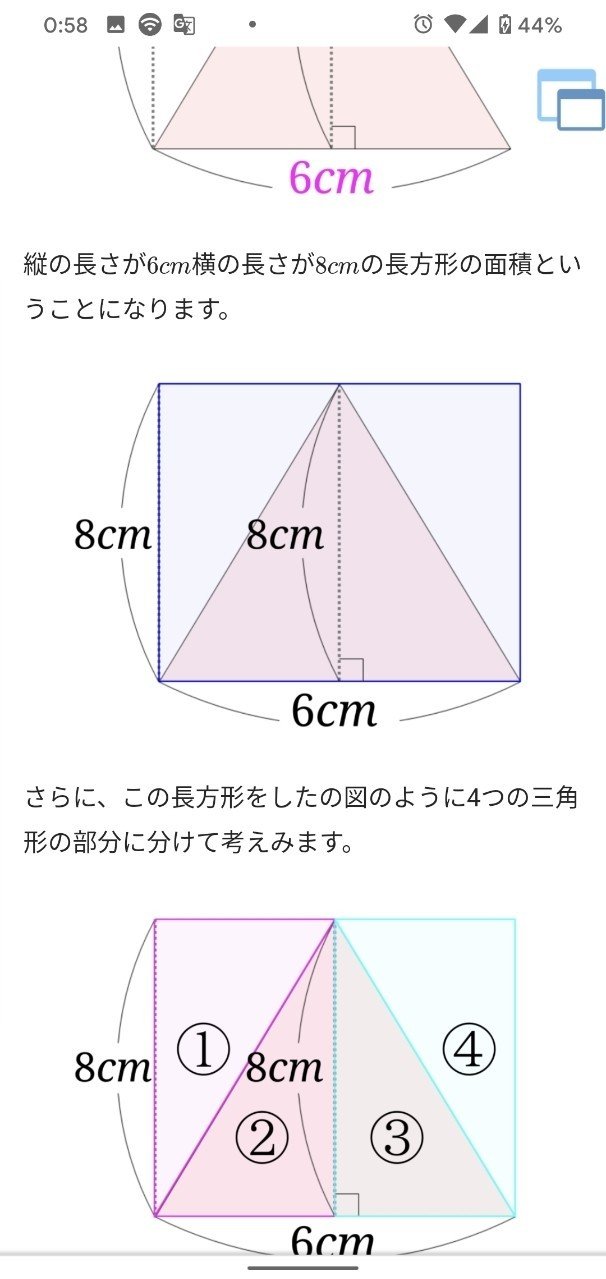



鈍角三角形の面積の求め方がやっと理解できたって話 猿田助 Note



3分なるほど 三角形の内角 外角の性質について解説 数スタ
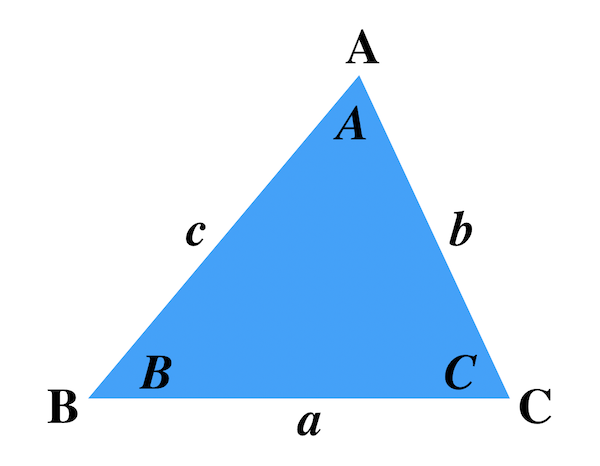



三角比 正弦定理と余弦定理を詳しく解説 スタディクラブ情報局




華奢デザインが ネックレスやピアスに ハンドメイド 金具 材料 素材 修理 初心者 通販 メタルパーツ レジン 鋭角三角形のフレームパーツ 16 40mm 6個セット メール便対応 ハンドメイドパーツ ビーズ ピアス アクセサリーパーツ ビンテージ ヴィンテージ風
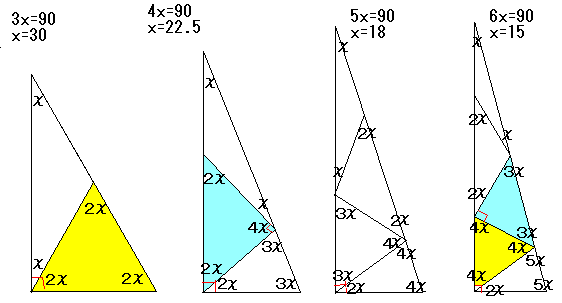



はしご直角三角形



数学教師向け 平面図形問題の作成ための無料作図ソフト



直角三角形と証明 中学2年 数学クラブ




正三角形 直角三角形 の韓国語は 三角形の種類や特徴を表現してみよう 気になるkorean




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強




東京大 座標上の鋭角三角形 鈴木貫太郎 Official Website




三角形の成立条件と鋭角 直角 鈍角三角形の判定 数学の偏差値を上げて合格を目指す



Kadai78




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強



1




直角三角形の辺の長さ 合同条件 面積について アタリマエ
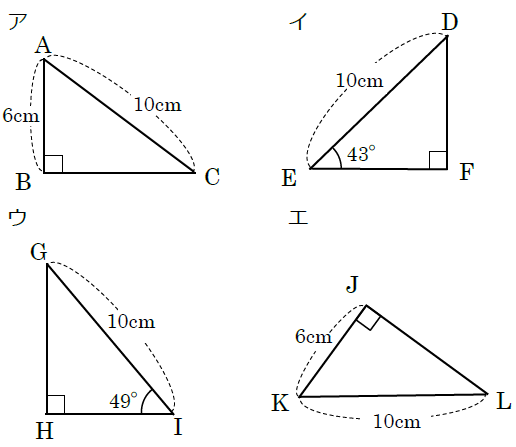



中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン



三角形の種類 算数勉強会 小学 楽天ブログ



鋭角三角形とは 1分でわかる意味 条件 直角三角形 鈍角三角形との違い
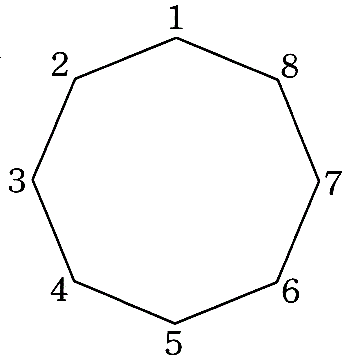



直撃 中学入試問題 第154回 山手学院中 場合の数 正八角形の頂点を結んでできる三角形 北辰塾 情報局



Www Kyoto Be Ne Jp Rakuhoku Hs Buildupload Pdffile Pdf



Www Kyoto Be Ne Jp Rakuhoku Hs Buildupload Pdffile Pdf




鋭角三角形 直角三角形 鈍角三角形かを調べる方法 数学i By ふぇるまー マナペディア
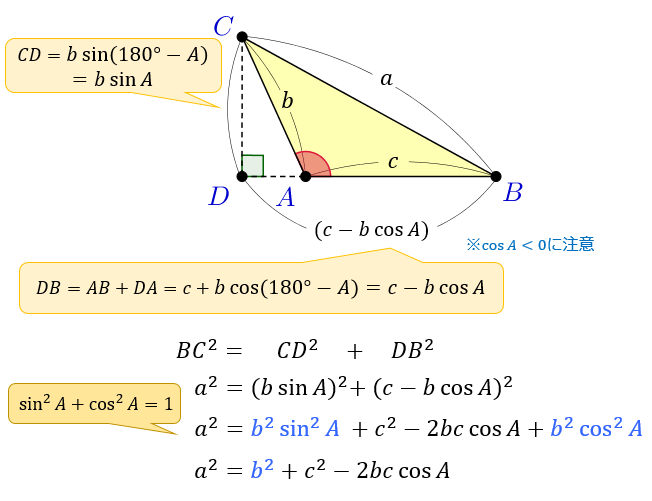



余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




正十二角形の3点を結んでできる三角形の個数 種類別 数学の偏差値を上げて合格を目指す




中2数学 三角形の内角と外角の定期テスト過去問分析問題 Atstudier




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学




正十二角形の3点を結んでできる三角形の個数 種類別 数学の偏差値を上げて合格を目指す




中学数学 平面図形と平行線の性質




03 号 可変面積型荷電粒子ビーム描画方法及び可変面積型荷電粒子ビーム描画装置 Astamuse



1




タンジェントとは何か 中学生でも分かる三角関数の基礎



鈍角三角形の分割




14 号 図形板セット Astamuse



Triangles




三角形の種類を判定しよう 電験3種web
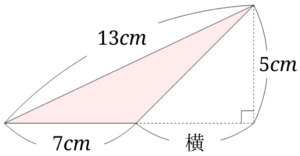



三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校



全て の 角 が 90 の 三角形




Amazon Co Jp 1枚で 平面図形 がわかる Learneasy 図形 を学ぼう 平面図形の種類と公式ポスター プチバイリンガル英語付き 大判a2サイズ 一覧表 小学生算数教材 文房具 オフィス用品



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典



Basicプログラミング




鋭角 鋭角 えいかく の意味翻譯此網頁 Charlie W
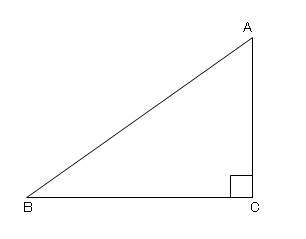



いろいろな三角形 3 ネット塾



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典
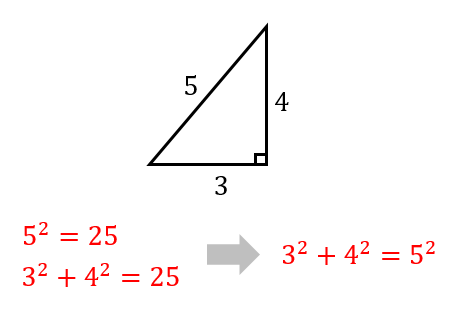



鋭角 鈍角三角形 三平方の定理を使って見分ける方法を解説 数スタ




三角形 Wikipedia




図形 三角形 01のイラスト素材



Http Suusenn Com Column Edex M85 M85sample M8502g Pdf
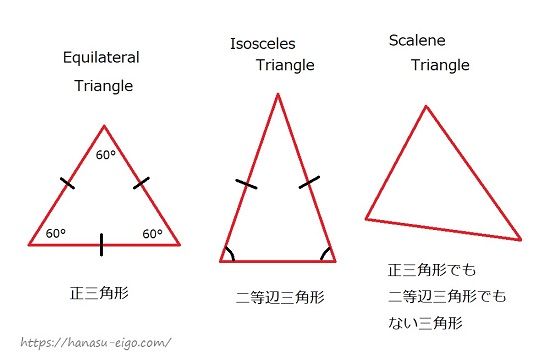



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語



48s96ub7b0z5f Net Sankakuhi Seiritsujouken Katachi
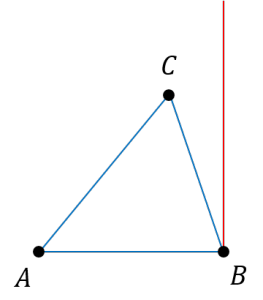



質問 数学a 図形 三角形に外接円が必ず存在する理由 オンライン無料塾 ターンナップ



3



鋭角三角形の確率



図形の調べ方 三角形についてまるわかり 苦手な数学を簡単に




三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校
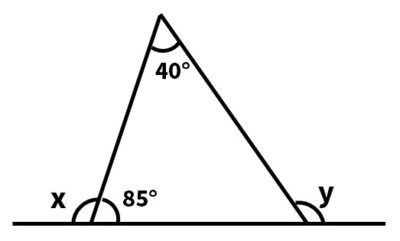



中2数学 三角形の内角と外角の定期テスト過去問分析問題 Atstudier




三角形の種類 算数勉強会 小学 楽天ブログ



1




中2数学 鋭角三角形 鈍角三角形 直角三角形とは 小学生 中学生の勉強
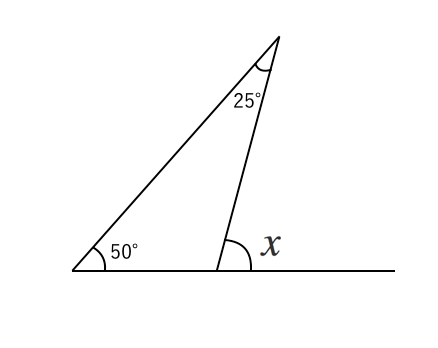



図形の調べ方 三角形についてまるわかり 苦手な数学を簡単に




鋭角三角形と鈍角三角形の意味と見分け方 具体例で学ぶ数学
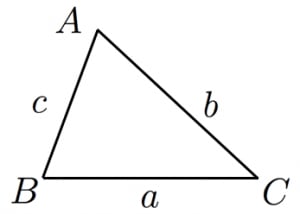



Sinを用いた三角形の面積公式 高校数学の美しい物語




高校数学 三角形の鋭角 直角 鈍角条件 三角形の成立条件3パターン 受験の月




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン




鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく
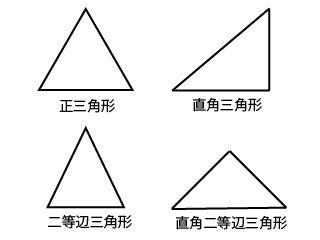



三角形の計算 もう一度やり直しの算数 数学




鋭角三角形と鈍角三角形をみわける3つのステップ Qikeru 学びを楽しくわかりやすく



図形の問題です 図のように 鋭角三角形abcの頂点aか Yahoo 知恵袋




二等辺三角形や直角三角形って英語で何て言うの 三角形の種類について 40代 50代 60代 シニア 初心者からやり直し英会話 英語学習法



外接円 外心について



全て の 角 が 90 の 三角形




三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語



鋭角三角形実際にかわいい三角形 ポスター Zazzle Co Jp




中2数学 鋭角 鈍角とはいったい何ものなのか Qikeru 学びを楽しくわかりやすく




数学 中2 50 鋭角三角形と鈍角三角形 Youtube



Gdp Mmy0vb5 4m




高校数学a 正多角形内の三角形の個数 二等辺三角形 正三角形 直角三角形 鈍角三角形 鋭角三角形他 受験の月



全て の 角 が 90 の 三角形



外接円 外心について




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学
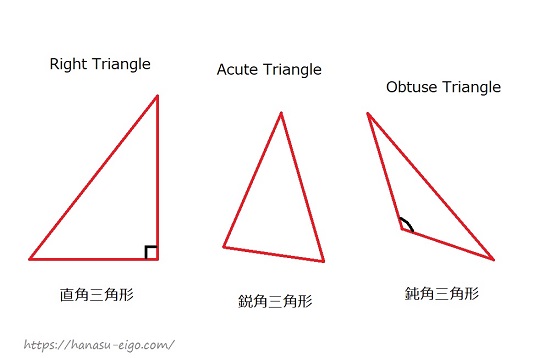



三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語



直角 鋭角 鈍角三角形の判定法 思考力を鍛える数学



三平方の定理 規則集3 中学から数学だいすき



Studydoctor三角形の内角と分類 中2数学 Studydoctor



高校数a 図形 鋭角三角形 鈍角三角形の判別方法 オンライン無料塾 ターンナップ Youtube




中2数学 鋭角三角形 鈍角三角形 直角三角形とは 小学生 中学生の勉強




数学ia 三角形の形状決定問題 大学入試数学の考え方と解法



Basicプログラミング
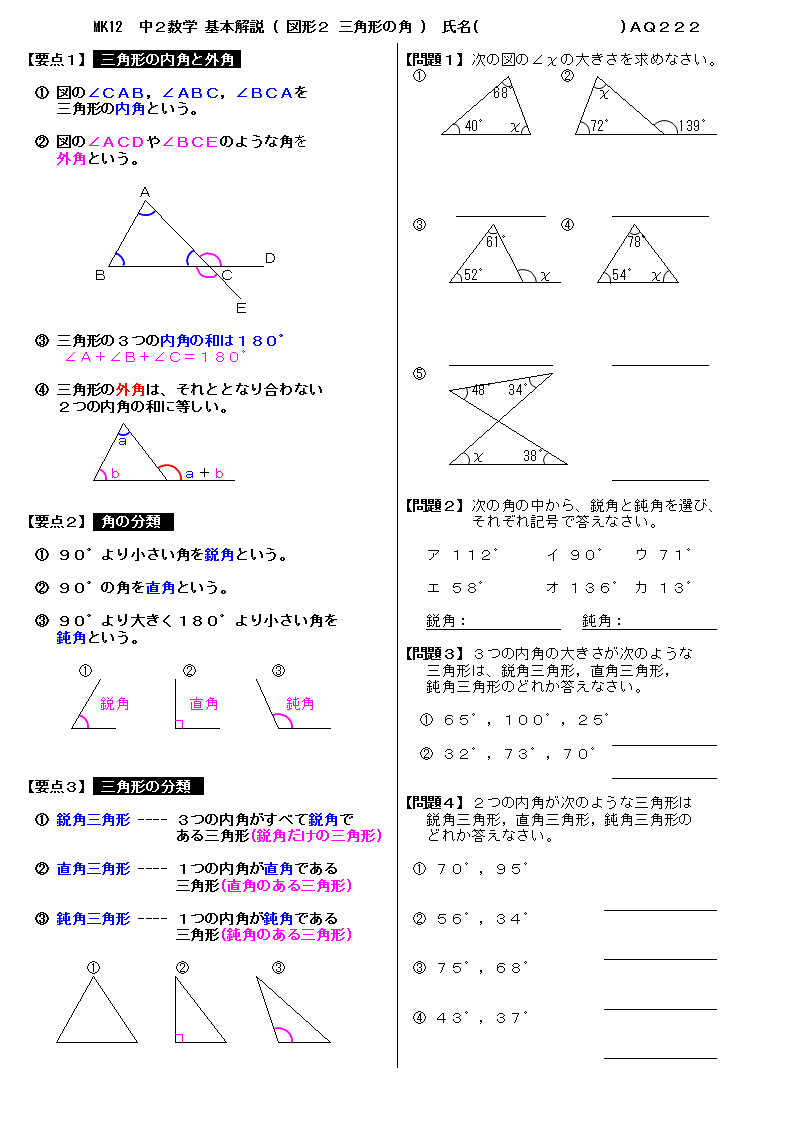



無料 中2数学 基本解説 問題プリント 222 図形2 三角形の角



直角三角形の合同条件




三角形 膨大なページ数 Wiki




14 号 図形板セット Astamuse


